Limitations of Gödel Machines

The fundamental limitations are closely related to those first identified by Gödel's celebrated paper on self-referential formulae [11]. Any formal system that encompasses arithmetics (or ZFC etc) is either flawed or allows for unprovable but true statements. Hence even a Gödel machine with unlimited computational resources must ignore those self-improvements whose effectiveness it cannot prove, e.g., for lack of sufficiently powerful axioms in 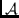$\cal A$. In particular, one can construct pathological examples of environments and utility functions that make it impossible for the machine to ever prove a target theorem. Compare Blum's speed-up theorem [3,4] based on certain incomputable predicates. Similarly, a realistic Gödel machine with limited resources cannot profit from self-improvements whose usefulness it cannot prove within its time and space constraints.

Nevertheless, unlike previous methods, it can in principle exploit at least the provably good speed-ups of any part of its initial software, including those parts responsible for huge (but problem class-independent) slowdowns ignored by the earlier approaches [16,17] (Section 6.4).