


Next: Basic Idea of Gödel
Up: Overview / Basic Ideas
Previous: Overview / Basic Ideas
Set-up and Formal Goal
Our hardware (e.g., a universal or space-bounded
Turing machine
[56]
or the abstract model
of a personal computer)
has a single life which
consists of discrete cycles or time steps
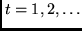 .
Its total lifetime
.
Its total lifetime 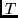 may or may not be known in advance.
In what follows, the value of any time-varying variable
may or may not be known in advance.
In what follows, the value of any time-varying variable 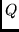 at time
at time 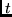 will be denoted by
will be denoted by 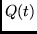 .
.
During each cycle our hardware
executes an elementary operation which affects its
variable state
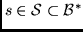 (without loss of generality,
(without loss of generality, 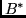 is
the set of possible bitstrings over
the binary alphabet
is
the set of possible bitstrings over
the binary alphabet 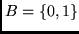 )
and possibly also the variable environmental state
)
and possibly also the variable environmental state
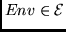 (here we need not yet specify the problem-dependent set
(here we need not yet specify the problem-dependent set 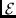 ).
There is a hardwired
state transition function
).
There is a hardwired
state transition function
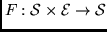 .
For
.
For 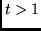 ,
,
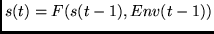 is the state at a point where
the hardware operation of cycle
is the state at a point where
the hardware operation of cycle 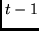 is finished, but the one of
is finished, but the one of
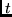 has not started yet.
has not started yet.
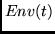 may depend on past output actions encoded in
may depend on past output actions encoded in 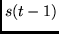 and
is simultaneously updated or (probabilistically) computed by
the possibly reactive environment.
and
is simultaneously updated or (probabilistically) computed by
the possibly reactive environment.
In order to talk conveniently about programs and data,
we will often attach names to certain string variables encoded
as components or substrings of 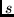 .
Of particular interest are the three variables called
time, x, y, and p:
.
Of particular interest are the three variables called
time, x, y, and p:
- At time
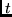 , variable
, variable 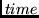 holds a unique binary representation of
holds a unique binary representation of 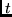 .
We initialize
.
We initialize
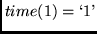 , the bitstring consisting only of a one.
The hardware increments
, the bitstring consisting only of a one.
The hardware increments 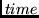 from one cycle to the next.
This requires at most
from one cycle to the next.
This requires at most 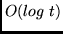 and on average only
and on average only 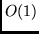 computational steps.
computational steps.
- Variable x holds the inputs form the environment to the Gödel machine.
For
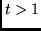 ,
, 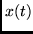 may
differ from
may
differ from 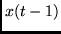 only if
a program running on the Gödel machine has executed
a special input-requesting instruction at time
only if
a program running on the Gödel machine has executed
a special input-requesting instruction at time 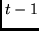 .
Generally speaking, the delays between successive inputs
should be sufficiently large so that
programs can perform
certain elementary computations on an input, such as copying
it into internal storage (a reserved part of
.
Generally speaking, the delays between successive inputs
should be sufficiently large so that
programs can perform
certain elementary computations on an input, such as copying
it into internal storage (a reserved part of 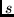 )
before the next input arrives.
)
before the next input arrives.
- Variable y holds the outputs of the Gödel machine.
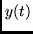 is an output bitstring which may
subsequently influence the
environment, where
is an output bitstring which may
subsequently influence the
environment, where
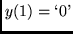 by default.
For example,
by default.
For example, 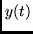 could be interpreted as a control
signal for an environment-manipulating
robot whose actions may have an effect on
future inputs.
could be interpreted as a control
signal for an environment-manipulating
robot whose actions may have an effect on
future inputs.
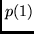 is the initial software: a program
implementing the original (sub-optimal) policy
for interacting with the environment,
represented as a substring
is the initial software: a program
implementing the original (sub-optimal) policy
for interacting with the environment,
represented as a substring 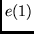 of
of 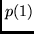 ,
plus the original policy for searching proofs.
Details will be discussed below.
,
plus the original policy for searching proofs.
Details will be discussed below.
At any given time 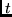 (
(
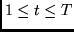 ) the goal
is to maximize future success or utility.
A typical ``value to go'' utility function
is of the form
) the goal
is to maximize future success or utility.
A typical ``value to go'' utility function
is of the form
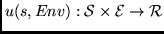 , where
, where
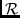 is the set of real numbers:
is the set of real numbers:
![\begin{displaymath}
u(s, Env) =
E_{\mu} \left [ \sum_{\tau=time}^{E_{\mu}(T \mid s, Env)} r(\tau)~~ \Bigg\vert ~~s, Env \right ],
\end{displaymath}](img35.png) |
(1) |
where 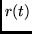 is a real-valued reward input (encoded within
is a real-valued reward input (encoded within 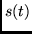 ) at time
) at time 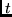 ,
,
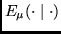 denotes the conditional expectation operator
with respect to some possibly unknown distribution
denotes the conditional expectation operator
with respect to some possibly unknown distribution 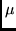 from a set
from a set 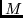 of possible distributions (
of possible distributions (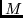 reflects
whatever is known about the possibly probabilistic reactions
of the environment), and the above-mentioned
reflects
whatever is known about the possibly probabilistic reactions
of the environment), and the above-mentioned 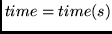 is a function
of state
is a function
of state 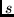 which uniquely identifies the
current cycle.
Note that we take into account the possibility of extending
the expected lifespan
which uniquely identifies the
current cycle.
Note that we take into account the possibility of extending
the expected lifespan
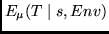 through appropriate actions.
through appropriate actions.
Alternative formalizable utility functions could favor
improvement of worst case instead
of expected future performance,
or higher reward intake per time interval etc.
Clearly, most classic problems of computer science
can be formulated in this framework--see examples
in Section 6.2.



Next: Basic Idea of Gödel
Up: Overview / Basic Ideas
Previous: Overview / Basic Ideas
Juergen Schmidhuber
2005-01-03
![]() (without loss of generality,
(without loss of generality, ![]() is
the set of possible bitstrings over
the binary alphabet
is
the set of possible bitstrings over
the binary alphabet ![]() )
and possibly also the variable environmental state
)
and possibly also the variable environmental state
![]() (here we need not yet specify the problem-dependent set
(here we need not yet specify the problem-dependent set ![]() ).
There is a hardwired
state transition function
).
There is a hardwired
state transition function
![]() .
For
.
For ![]() ,
,
![]() is the state at a point where
the hardware operation of cycle
is the state at a point where
the hardware operation of cycle ![]() is finished, but the one of
is finished, but the one of
![]() has not started yet.
has not started yet.
![]() may depend on past output actions encoded in
may depend on past output actions encoded in ![]() and
is simultaneously updated or (probabilistically) computed by
the possibly reactive environment.
and
is simultaneously updated or (probabilistically) computed by
the possibly reactive environment.
![]() .
Of particular interest are the three variables called
time, x, y, and p:
.
Of particular interest are the three variables called
time, x, y, and p:
![]() (
(
![]() ) the goal
is to maximize future success or utility.
A typical ``value to go'' utility function
is of the form
) the goal
is to maximize future success or utility.
A typical ``value to go'' utility function
is of the form
![]() , where
, where
![]() is the set of real numbers:
is the set of real numbers: