


Next: EXPERIMENTAL RESULTS
Up: DERIVATION OF THE ALGORITHM
Previous: DERIVATION OF THE ALGORITHM
Let us assume a sender wants to send a description of
the function induced by 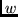 to a receiver who knows the inputs
to a receiver who knows the inputs 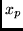 but not the targets
but not the targets  , where
, where
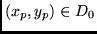 .
The MDL principle suggests that the
sender wants to minimize the
expected description length of the net function.
Let
.
The MDL principle suggests that the
sender wants to minimize the
expected description length of the net function.
Let
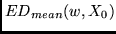 denote the mean value of
denote the mean value of  on the box.
Expected description length
is approximated by
on the box.
Expected description length
is approximated by
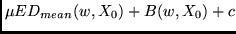 ,
where
,
where 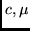 are positive constants.
One way of seeing this is
to apply Hinton and van Camp's
``bits back'' argument
to a uniform weight prior
(
are positive constants.
One way of seeing this is
to apply Hinton and van Camp's
``bits back'' argument
to a uniform weight prior
(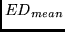 corresponds to the output variance).
However, we prefer to use a different argument:
we encode each weight
corresponds to the output variance).
However, we prefer to use a different argument:
we encode each weight 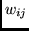 of the box center
of the box center 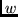 by a bitstring
according to the following procedure
(
by a bitstring
according to the following procedure
( is given):
is given):
(0) Define a variable interval
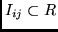 .
.
(1) Make 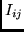 equal to the interval constraining possible
weight values.
equal to the interval constraining possible
weight values.
(2) While
![$I_{ij} \not\subset [w_{ij}-\Delta w_{ij}, w_{ij} + \Delta w_{ij}]$](img103.png) :
:
Divide 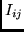 into
2 equally-sized disjunct intervals
into
2 equally-sized disjunct intervals  and
and 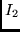 .
.
If
 then
then
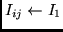 ; write `1'.
; write `1'.
If
 then
then
 ; write `0'.
; write `0'.
The final set 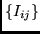 corresponds to a ``bit-box'' within our box.
This ``bit-box'' contains
corresponds to a ``bit-box'' within our box.
This ``bit-box'' contains
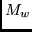 's center
's center 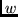 and is described by a bitstring of length
and is described by a bitstring of length
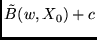 , where the constant
, where the constant 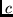 is independent of
the box
is independent of
the box 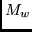 . From
. From
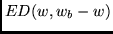 (
( is the center of the ``bit-box'')
and the bitstring describing the ``bit-box'',
the receiver can compute
is the center of the ``bit-box'')
and the bitstring describing the ``bit-box'',
the receiver can compute 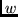 as follows:
he selects an initialization
weight vector within the ``bit-box'' and
uses gradient descent
to decrease
as follows:
he selects an initialization
weight vector within the ``bit-box'' and
uses gradient descent
to decrease  until
until
 , where
, where
 in the bit-box denotes the
receiver's current approximation of
in the bit-box denotes the
receiver's current approximation of  (
( is constantly updated by the receiver).
This is like ``FMS without targets'' - recall that the
receiver knows the inputs
is constantly updated by the receiver).
This is like ``FMS without targets'' - recall that the
receiver knows the inputs 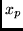 .
Since
.
Since 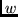 corresponds to the weight vector with the highest
degree of local flatness
within the ``bit-box'',
the receiver will find the correct
corresponds to the weight vector with the highest
degree of local flatness
within the ``bit-box'',
the receiver will find the correct 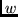 .
.
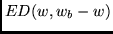 is described by a Gaussian distribution with mean zero.
Hence, the description length of
is described by a Gaussian distribution with mean zero.
Hence, the description length of 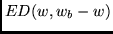 is
is
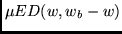 (Shannon, 1948).
(Shannon, 1948).
 , the center of the ``bit-box'',
cannot be known before training.
However, we do know the expected description length of
the net function, which is
, the center of the ``bit-box'',
cannot be known before training.
However, we do know the expected description length of
the net function, which is
 (
(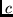 is a constant independent of
is a constant independent of 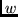 ).
Let us approximate
).
Let us approximate 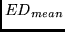 :
:

 .
.
Among those 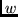 that lead to
equal
that lead to
equal 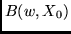 (the negative logarithm of
the box volume plus
(the negative logarithm of
the box volume plus  ),
we want to find those with minimal description length of
the function induced by
),
we want to find those with minimal description length of
the function induced by 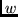 .
Using Lagrange multipliers (viewing the
.
Using Lagrange multipliers (viewing the 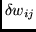 as variables),
it can be shown that
as variables),
it can be shown that 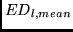 is minimal under the
condition
is minimal under the
condition
 iff flatness condition 2 holds.
To conclude: with given box volume, we need
flatness condition 2 to minimize the expected description length of
the function induced by
iff flatness condition 2 holds.
To conclude: with given box volume, we need
flatness condition 2 to minimize the expected description length of
the function induced by 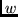 .
.



Next: EXPERIMENTAL RESULTS
Up: DERIVATION OF THE ALGORITHM
Previous: DERIVATION OF THE ALGORITHM
Juergen Schmidhuber
2003-02-13
Back to Financial Forecasting page
 .
.
![]() is described by a Gaussian distribution with mean zero.
Hence, the description length of
is described by a Gaussian distribution with mean zero.
Hence, the description length of ![]() is
is
![]() (Shannon, 1948).
(Shannon, 1948).
![]() , the center of the ``bit-box'',
cannot be known before training.
However, we do know the expected description length of
the net function, which is
, the center of the ``bit-box'',
cannot be known before training.
However, we do know the expected description length of
the net function, which is
![]() (
(![]() is a constant independent of
is a constant independent of ![]() ).
Let us approximate
).
Let us approximate ![]() :
:
![]()
 .
.
![]() that lead to
equal
that lead to
equal ![]() (the negative logarithm of
the box volume plus
(the negative logarithm of
the box volume plus ![]() ),
we want to find those with minimal description length of
the function induced by
),
we want to find those with minimal description length of
the function induced by ![]() .
Using Lagrange multipliers (viewing the
.
Using Lagrange multipliers (viewing the ![]() as variables),
it can be shown that
as variables),
it can be shown that ![]() is minimal under the
condition
is minimal under the
condition
![]() iff flatness condition 2 holds.
To conclude: with given box volume, we need
flatness condition 2 to minimize the expected description length of
the function induced by
iff flatness condition 2 holds.
To conclude: with given box volume, we need
flatness condition 2 to minimize the expected description length of
the function induced by ![]() .
.