


Next: The Architecture and the
Up: LEARNING TO CONTROL FAST-WEIGHT
Previous: LEARNING TO CONTROL FAST-WEIGHT
A training sequence 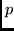 with
with 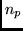 discrete time steps (called an episode)
consists
of
discrete time steps (called an episode)
consists
of 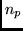 ordered pairs
ordered pairs
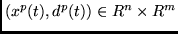 ,
,
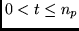 .
At time
.
At time 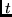 of episode
of episode 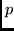 a learning system receives
a learning system receives 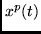 as
an input and produces the output
as
an input and produces the output 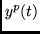 . The goal of the learning system
is to minimize
. The goal of the learning system
is to minimize
where 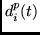 is the
is the  th of the
th of the 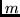 components of
components of 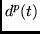 ,
and
,
and 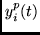 is the
is the  th of the
th of the 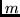 components of
components of 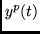 .
.
In general, this task requires
storage of input events in a short-term memory.
Previous solutions to this problem
have employed gradient-based dynamic recurrent nets
(e.g.,
[Robinson and Fallside, 1987],
[Pearlmutter, 1989],
[Williams and Zipser, 1989]).
In the next section an alternative gradient-based
approach is described. For convenience,
we drop the indices 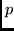 which stand for the various episodes.
which stand for the various episodes.
The gradient of the error over
all episodes is equal to the sum of the gradients for each episode.
Thus we only require a method for
minimizing the error observed during one particular episode:
where
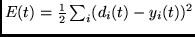 . (In the
practical on-line version of the algorithm below there will be
no episode boundaries; one episode will 'blend' into the next
[Williams and Zipser, 1989].)
. (In the
practical on-line version of the algorithm below there will be
no episode boundaries; one episode will 'blend' into the next
[Williams and Zipser, 1989].)



Next: The Architecture and the
Up: LEARNING TO CONTROL FAST-WEIGHT
Previous: LEARNING TO CONTROL FAST-WEIGHT
Juergen Schmidhuber
2003-02-13
Back to Recurrent Neural Networks page
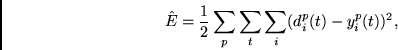
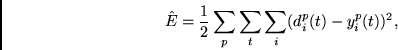
![]() which stand for the various episodes.
which stand for the various episodes.