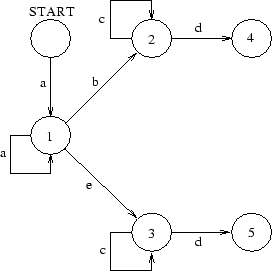
 |
Figure 1 shows a stochastic automaton for generating sequences. To produce a string of symbols, we begin in the start state. From there we move to state 1 and emit the symbol ``a''. In state 1 there is a choice of three alternatives: We can go to state 1 again and emit another ``a''. We can go to state 2 and emit a ``b''. We can go to state 3 and emit an ``e''. Whenever there are alternatives, the automaton selects among them with equal probability. States 4 and 5 are final states and correspond to sequence endings. We say that a sequence that ends in state 4 is of class 1. We say that a sequence that ends in state 5 is of class 2. Here are typical sequences of class 1: abcd, aaaaaaabcd, aaabccccccd. Here is a typical sequence of class 2: aaaeccccccd.
The goal for a (yet unspecified) sequence classifier is to read sequences, one symbol at a time, and to learn to classify them with respect to whether they belong to class 1 or class 2. The classifier does not know anything about the automaton. All it sees are the successive symbols and a teacher signal at the end of each sequence. The teacher signal provides the information about the desired classification. Consider the last two sequences examples above. They illustrate that the difference between class 1 and class 2 only depends on the first letter in the sequence that is not an ``a''. If this letter is a ``b'', then the sequence is of class 1. If this letter is an ``e'', then the sequence is of class 2. Therefore, the classifier somehow has to learn to store the occurrence of the first letter that is not an ``a'' and to memorize it for an unknown number of discrete time steps - until the end of the sequence is reached. Otherwise it will not be able to classify correctly.