Mathematische Details

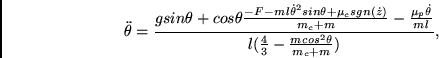
Details der Wagen/Stab Simulation

Das in den Kapiteln 4, 5, und 6 verwendete physikalische Wagen/Stab-System wurde durch folgende Differentialgleichungen modelliert:

$$\ddot{\theta} = \frac{g sin \theta + cos \theta \frac{- F... ...m l} } {l (\frac{4}{3} - \frac{m cos^{2}\theta}{m_{c} + m})},$$

$$\ddot{z} = \frac{F + m l (\dot{\theta}^{2}sin \theta - \ddot{\theta}cos \theta) - \mu_{c}sgn(\dot{z})} {m_{c} + m} .$$

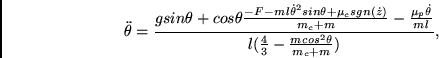
Dabei ist der Winkel des Stabes mit der Vertikalen, die Position des Wagens auf der Spur, die Gravitationsbeschleunigung, die Masse des Wagens, die Masse des Stabes, die halbe Stablänge, der Reibungskoeffizient des Wagens auf der Bahn, der Reibungskoeffizient des Stabes auf dem Wagen, bzw. für A1 bzw. für A2 die auf den Schwerpunkt des Wagens parallel zur Spur ausgeübte Kraft. (Man beachte, daß die in [5], [66] und [2] angegebenen Gleichungen einen Tippfehler enthalten: Dort wurde die Gravitationsbeschleunigung jeweils als definiert.)

Für A1 und A3 wurden u. a. folgende skalierte Eingabevariablen verwendet: , , , .

Für den modifizierten A2 gab es nur die beiden skalierten Eingabevariablen $\bar{z}$ und $\bar{\theta}$.

Weite Sprünge durch den Gewichtsraum im Falle spärlicher Codierung

Was uns beim Gradientenabstieg (siehe das Kapitel zum überwachten Lernen) wirklich interessiert, sind nicht so sehr die Minima, sondern die Nullstellen der Fehlerfunktion

$$E = \sum_p E_p ,$$

wobei $E_p$ der zu einem Eingabemusterpaar $p$ gehörige Fehler ist. BP liefert uns für alle $p$

$${\partial E_{p}}\over{\partial \vec{w}},$$

wobei $\vec{w}=(w_{1},..,w_{n})^T$ der komplette Gewichtsvektor des Netzes ist. Gradientenabstieg erfordert eine Gewichtsänderung

$$\bigtriangleup \vec{w} = -\eta \left( \frac{\partial E_{p}}{\partial \vec{w}} \right)^T,$$

wobei $\eta$ eine positive Lernrate ist. Was wir brauchen, ist eine gute Wahl für $\eta$. Wir berechnen $\eta$ für jede Musterpräsentation neu, so daß der geänderte Gewichtsvektor

$$\hat{\vec{w}}=\vec{w} + \bigtriangleup \vec{w}$$

auf den Schnitt der $n$-dimensionalen Gewichtshyperebene (im $n+1$-dimensionalen Gewichts-Fehler-Raum) mit der durch den gegenwärtigen Fehler und den gegenwärtigen Gradienten definierten Geraden zeigt. Die Grundannahme dabei ist, daß die $E_p$ lokal durch die tangentialen Hyperebenen approximiert werden können. (Man betrachte Abbildung A.1 für eine Illustration des eindimensionalen Falles.)

Etwas elementare Geometrie ergibt, daß für ein gegebenes $p$

$$\begin{eqnarray*} \eta = \frac{E_{p}}{\sum_{k} (\frac{\partial E_{p}}{\partial w_{k}})^{2}} \end{eqnarray*}$$

gelten muß, wobei $w_{i}$ das $i$-te Gewicht ist, und $k$ alle Gewichtsindizes durchläuft. Falls der Gradient verschwindet, so wird $\eta$ gleich Null gesetzt. In [49] wird experimentell an einigen Beispielen gezeigt, daß die Methode bei spärlicher Codierung zu einer bedeutenden Verringerung der Anzahl der Lernzyklen führen kann.

Abbildung: Illustration eines Iterationsschrittes für den Fall eines eindimensionalen Gewichtsvektors.

Related links in English: Recurrent neural networks - Subgoal learning - Reinforcement learning and POMDPs - Reinforcement learning economies - Selective attention
Deutsche Heimseite