Jede Fokustrajektorie schließt ![]() diskrete Zeitschritte 1 ...
diskrete Zeitschritte 1 ... ![]() ein.
Zum Zeitpunkt
ein.
Zum Zeitpunkt ![]() der Trajektorie
der Trajektorie ![]() heißt
heißt ![]() 's Eingabevektor
's Eingabevektor
![]() .
.
![]() ergibt sich aus den sensorischen Eingaben des Fokus zur Zeit
ergibt sich aus den sensorischen Eingaben des Fokus zur Zeit ![]() .
.
![]() 's Ausgabevektor zur Zeit
's Ausgabevektor zur Zeit ![]() heißt
heißt
![]() .
.
![]() wird als Steuersignal für den Fokus interpretiert und verursacht
eine Fokusbewegung und damit eine neue Eingabe
wird als Steuersignal für den Fokus interpretiert und verursacht
eine Fokusbewegung und damit eine neue Eingabe ![]() .
Die finale gewünschte Eingabe
.
Die finale gewünschte Eingabe ![]() der Trajektorie
der Trajektorie
![]() ist ein extern vorgegebenes Aktivationsmuster und korrespondiert zu
dem in der visuellen Szene zu findenden Objekt. Für alle
ist ein extern vorgegebenes Aktivationsmuster und korrespondiert zu
dem in der visuellen Szene zu findenden Objekt. Für alle ![]() ist
ist
![]() .
Zunächst nehmen wir an, daß
.
Zunächst nehmen wir an, daß
![]() für alle Trajektorien
für alle Trajektorien ![]() konstant ist (es soll also immer
dasselbe Detail der Szene gefunden werden).
konstant ist (es soll also immer
dasselbe Detail der Szene gefunden werden).
![]() 's Aufgabe besteht darin, startend von beliebig vorgegebenen
Anfangspositionen Sequenzen von Fokusbewegungen zu produzieren, so daß
für alle Trajektorien
's Aufgabe besteht darin, startend von beliebig vorgegebenen
Anfangspositionen Sequenzen von Fokusbewegungen zu produzieren, so daß
für alle Trajektorien ![]() gilt:
gilt:
![]() .
Der finale Eingabefehler
.
Der finale Eingabefehler
![]() der zum Zeitschritt
der zum Zeitschritt ![]() unterbrochenen Trajektorie
unterbrochenen Trajektorie ![]() ist
ist
Die ![]() ergeben sich also aus den Differenzen zwischen den
gewünschten und den tatsächlichen finalen Eingaben.
ergeben sich also aus den Differenzen zwischen den
gewünschten und den tatsächlichen finalen Eingaben.
Das Modellnetzwerk ![]() sieht zu einem gegebenen Zeitpunkt
sieht zu einem gegebenen Zeitpunkt ![]()
![]() 's Ein- und Ausgabe und wird
darauf trainiert,
's Ein- und Ausgabe und wird
darauf trainiert, ![]() 's nächste Eingabe zu prophezeien.
Die folgende Diskussion bezieht sich auf den Fall, daß
's nächste Eingabe zu prophezeien.
Die folgende Diskussion bezieht sich auf den Fall, daß
![]() und
und ![]() parallel lernen. In einigen Experimenten werden
wir separate Trainingsphasen für
parallel lernen. In einigen Experimenten werden
wir separate Trainingsphasen für ![]() und
und ![]() verwenden,
die Änderungen für diesen Fall sind aber trivial und
hauptsächlich notationeller Art.
verwenden,
die Änderungen für diesen Fall sind aber trivial und
hauptsächlich notationeller Art.
![]() 's Eingabevektor zur Zeit
's Eingabevektor zur Zeit ![]() der Trajektorie
der Trajektorie ![]() ist die Konkatenation von
ist die Konkatenation von
![]() und
und ![]() .
.
![]() 's Ausgabevektor zur Zeit
's Ausgabevektor zur Zeit ![]() der Trajektorie
der Trajektorie ![]() ist
ist ![]() ,
wobei
,
wobei
![]() .
.
![]() 's Fehler zur Zeit
's Fehler zur Zeit ![]() der Trajektorie
der Trajektorie ![]() ist
ist
![]() 's Ziel ist die Minimierung von
's Ziel ist die Minimierung von
![]() ,
wozu BP verwendet wird:
,
wozu BP verwendet wird:
Dem Systemidentifikationsansatz folgend nehmen wir nun an, daß
![]() durch eine differenzierbare Funktion von
durch eine differenzierbare Funktion von ![]() 's
Gewichtsvektor
's
Gewichtsvektor ![]() angenähert werden kann.
Um
angenähert werden kann.
Um
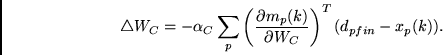
Dabei ist ![]() das Inkrement von
das Inkrement von ![]() und
und
![]()
![]() 's Lernrate.
Man beachte, daß die Differenz zwischen der
gewünschten finalen Eingabe und der tatsächlichen finalen
Eingabe zur Berechnung eines Gradienten für
's Lernrate.
Man beachte, daß die Differenz zwischen der
gewünschten finalen Eingabe und der tatsächlichen finalen
Eingabe zur Berechnung eines Gradienten für ![]() unter
Zuhilfenahme von
unter
Zuhilfenahme von ![]() herangezogen wird, nicht die Differenz
zwischen
der gewünschten finalen Eingabe und der von
herangezogen wird, nicht die Differenz
zwischen
der gewünschten finalen Eingabe und der von ![]() vorhergesagten
finalen Eingabe (siehe auch Kapitel 6).
(In den unten beschriebenen Experimenten weichen wir
vom reinen Gradientenabstieg ab und ändern
vorhergesagten
finalen Eingabe (siehe auch Kapitel 6).
(In den unten beschriebenen Experimenten weichen wir
vom reinen Gradientenabstieg ab und ändern ![]() 's Gewichte
am Ende jeder Trajektorie.)
's Gewichte
am Ende jeder Trajektorie.)