Test all programssuch that
, the maximal time spent on creating and running and testing
, satisfies
.
Set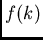
The following straight-forward method (sometimes referred to as Levin Search or LSEARCH) is near-bias-optimal. For simplicity, we notationally suppress conditional dependencies on the current problem. Compare Levin ([30,32] --Levin also attributes similar ideas to Adleman), [69], [65], [33], [20].
Test all programssuch that
, the maximal time spent on creating and running and testing
, satisfies
.
Set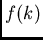
The near-bias-optimality of LSEARCH
is hardly affected by the fact that for each value of ![]() we
repeat certain computations for the previous value.
Roughly half the total search time is still spent on
we
repeat certain computations for the previous value.
Roughly half the total search time is still spent on ![]() 's maximal
value (ignoring hardware-specific overhead for parallelization and
nonessential speed-ups due to halting programs
if there are any).
Note also that the time for testing is properly taken into account here:
any result whose validity is hard to test is automatically penalized.
's maximal
value (ignoring hardware-specific overhead for parallelization and
nonessential speed-ups due to halting programs
if there are any).
Note also that the time for testing is properly taken into account here:
any result whose validity is hard to test is automatically penalized.
Nonuniversal variants. LSEARCH provides inspiration for nonuniversal but very practical methods which are optimal with respect to a limited search space, while suffering only from very small slowdown factors. For example, designers of planning procedures often just face a binary choice between two options such as depth-first and breadth-first search. The latter is often preferrable, but its greater demand for storage may eventually require to move data from on-chip memory to disk. This can slow down the search by a factor of 10,000 or more. A straightforward solution in the spirit of LSEARCH is to start with a 50 % bias towards either technique, and use both depth-first and breadth-first search in parallel -- this will cause a slowdown factor of at most 2 with respect to the best of the two options (ignoring a bit of overhead for parallelization). Such methods have presumably been used long before Levin's 1973 paper. [80] and [65] used rather general but nonuniversal variants of LSEARCH to solve machine learning toy problems unsolvable by traditional methods. Probabilistic alternatives based on probabilistically chosen maximal program runtimes in Speed-Prior style [54,58] also outperformed traditional methods on toy problems [52,53].