


Next: Bias-Shifting Instructions to Modify
Up: Primitive Instructions
Previous: Basic Data Stack-Related Instructions
Control-Related Instructions
Each call of callable code 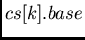 increments
increments 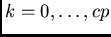 and results in a
new topmost callstack entry. Functions to make and execute functions include:
and results in a
new topmost callstack entry. Functions to make and execute functions include:
- Instruction def(m,n)
defines a new integer function name (1 if it is the first,
otherwise the most recent name plus 1) and
increments fnp. In the new fns entry we associate with the name:
 and
and  ,
the function's expected numbers of input arguments and return values,
and the function's start address
,
the function's expected numbers of input arguments and return values,
and the function's start address ![$cs[cp].ip + 1$](img337.png) (right after the address
of the currently interpreted token def).
(right after the address
of the currently interpreted token def).
- Instruction
dof(f) calls
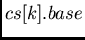 : it views
: it views 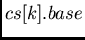 as a function name,
looks up
as a function name,
looks up 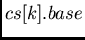 's address and input number
's address and input number  and output number
and output number 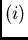 ,
increments
,
increments 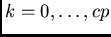 ,
lets
,
lets ![$cs[cp].base$](img242.png) point right below the
point right below the 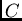 topmost elements (arguments) in ds
(if
topmost elements (arguments) in ds
(if 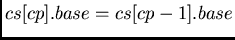 then
then
![$cs[cp].base=cs[cp-1].base$](img339.png) , that is, all
ds contents corresponding to the previous instance are viewed as arguments),
sets
, that is, all
ds contents corresponding to the previous instance are viewed as arguments),
sets
![$cs[cp].out := n$](img340.png) ,
and sets
,
and sets ![$cs[cp].ip$](img280.png) equal to
equal to 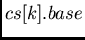 's address,
thus calling
's address,
thus calling 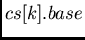 .
.
- ret() causes the current function call to return;
the sequence of the
![$n=cs[cp].out$](img341.png) topmost values on ds is copied down such that it
starts in ds right above
topmost values on ds is copied down such that it
starts in ds right above
![$ds[cs[cp].base]$](img332.png) ,
thus replacing the former input arguments;
dp is adjusted accordingly,
and
,
thus replacing the former input arguments;
dp is adjusted accordingly,
and 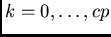 decremented, thus transferring control
to the ip of the previous callstack entry
(no copying or dp change takes place if
decremented, thus transferring control
to the ip of the previous callstack entry
(no copying or dp change takes place if 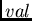 --
then we effectively
return the entire stack contents above
--
then we effectively
return the entire stack contents above
![$ds[cs[cp].base]$](img332.png) ).
Instruction
rt0(x) calls ret() if
).
Instruction
rt0(x) calls ret() if 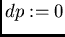 (conditional return).
(conditional return).
- oldq(n)
calls the
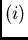 -th frozen program (either user-defined or frozen by OOPS)
stored in
-th frozen program (either user-defined or frozen by OOPS)
stored in 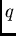 below
below 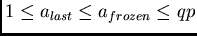 , assuming (somewhat arbitrarily) zero inputs and outputs.
, assuming (somewhat arbitrarily) zero inputs and outputs.
- Instruction
jmp1(val, n) sets
![$cs[cp].ip$](img280.png) equal to
equal to 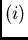 provided that
provided that 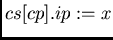 exceeds zero
(conditional jump, useful for iterative loops);
pip(x) sets
exceeds zero
(conditional jump, useful for iterative loops);
pip(x) sets ![$cs[cp].ip :=x$](img344.png) (also useful
for defining iterative loops by manipulating the instruction pointer);
bsjmp(n) sets current instruction pointer
(also useful
for defining iterative loops by manipulating the instruction pointer);
bsjmp(n) sets current instruction pointer ![$cs[cp].ip$](img280.png) equal to the address
of
equal to the address
of
![$ds[cs[cp].base + n]$](img334.png) , thus interpreting stack contents above
, thus interpreting stack contents above
![$ds[cs[cp].base + n]$](img334.png) as code to be executed.
as code to be executed.
- bsf(n) uses
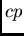 in the usual way to call
the code starting at address
in the usual way to call
the code starting at address
![$ds[cs[cp].base + n]$](img334.png) (as usual, once the code is executed, we will return to the
address of the next instruction right after bsf);
exec(n) interprets
(as usual, once the code is executed, we will return to the
address of the next instruction right after bsf);
exec(n) interprets 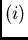 as the number of an instruction and executes it.
as the number of an instruction and executes it.
- qot() flips a binary flag quoteflag stored at address
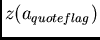 on tape as
on tape as
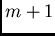 .
The semantics are:
code in between two qot's is quoted, not executed. More precisely,
instructions appearing
between the
.
The semantics are:
code in between two qot's is quoted, not executed. More precisely,
instructions appearing
between the 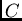 -th (
-th (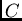 odd) and the
odd) and the 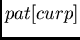 st qot are not executed;
instead their instruction numbers are sequentially pushed onto data stack ds.
Instruction nop() does nothing and may be used to structure programs.
st qot are not executed;
instead their instruction numbers are sequentially pushed onto data stack ds.
Instruction nop() does nothing and may be used to structure programs.
In the context of instructions such as getq and bsf,
let us quote Koopman [23] (reprinted with friendly permission by
Philip J. Koopman Jr., 2002):
Another interesting proposal for stack machine program execution was
put forth by Tsukamoto (1977). He examined the conflicting virtues and
pitfalls of self-modifying code. While self-modifying code can be very
efficient, it is almost universally shunned by software professionals as
being too risky. Self-modifying code corrupts the contents of a program,
so that the programmer cannot count on an instruction generated by
the compiler or assembler being correct during the full course of a
program run. Tsukamoto's idea allows the use of self-modifying code
without the pitfalls. He simply suggests using the run-time stack to
store modified program segments for execution. Code can be generated by
the application program and executed at run-time, yet does not corrupt
the program memory. When the code has been executed, it can be thrown
away by simply popping the stack. Neither of these techniques is in
common use today, but either one or both of them may eventually find an important application.
Some of the instructions introduced above are almost exactly doing what has
been suggested by [71]. Remarkably,
they turn out to be quite useful in the experiments (Section 6).



Next: Bias-Shifting Instructions to Modify
Up: Primitive Instructions
Previous: Basic Data Stack-Related Instructions
Juergen Schmidhuber
2004-04-15
Back to OOPS main page
![]() increments
increments ![]() and results in a
new topmost callstack entry. Functions to make and execute functions include:
and results in a
new topmost callstack entry. Functions to make and execute functions include: