| Symbol |
Description |
|
|
|
|
|
| ds |
data stack holding arguments of functions, possibly also edited code |
|
|
|
|
|
| dp |
stack pointer of ds |
|
|
|
|
|
| Ds |
auxiliary data stack |
|
|
|
|
|
| Dp |
stack pointer of Ds |
|
|
|
|
|
| cs |
call stack or runtime stack to handle function calls |
|
|
|
|
|
| cp |
stack pointer of cs |
|
|
|
|
|
![$cs[cp].ip$](img280.png) |
current function call's instruction pointer
.ip$](img281.png) |
|
|
|
|
|
![$cs[cp].base$](img242.png) |
current base pointer into ds right below the current input arguments |
|
|
|
|
|
![$cs[cp].out$](img282.png) |
number of return values expected on top of ds above ![$cs[cp].base$](img242.png) |
|
|
|
|
|
| fns |
stack of currently available self-made functions |
|
|
|
|
|
| fnp |
stack pointer of fns |
|
|
|
|
|
![$fns[fnp].code$](img283.png) |
start address of code of most recent self-made function |
|
|
|
|
|
![$fns[fnp].in$](img284.png) |
number of input arguments of most recent self-made function |
|
|
|
|
|
![$fns[fnp].out$](img285.png) |
number of return values of most recent self-made function |
|
|
|
|
|
| pats |
stack of search patterns (probability distributions on 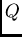 ) ) |
|
|
|
|
|
| patp |
stack pointer of pats |
|
|
|
|
|
| curp |
pointer to current search pattern in pats,
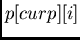 |
|
|
|
|
|
![$p[curp][i]$](img287.png) |
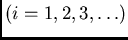 -th numerator of current search pattern -th numerator of current search pattern |
|
|
|
|
|
![$sum[curp]$](img288.png) |
denominator; the current probability of  is is
![$p[curp][i] / sum[curp]$](img289.png) |
|
|
|
|
|
![]() contains various stack-like data structures represented
as sequences of integers.
For any stack
contains various stack-like data structures represented
as sequences of integers.
For any stack ![]() introduced below
(here
introduced below
(here ![]() stands for a character string reminiscent of the stack type)
there is a (frequently not even mentioned) stack
pointer
stands for a character string reminiscent of the stack type)
there is a (frequently not even mentioned) stack
pointer ![]() ;
;
![]() ,
located at address
,
located at address ![]() , and initialized by 0.
The
, and initialized by 0.
The ![]() -th element of
-th element of ![]() is denoted
is denoted ![]() .
For simplicity we will often omit tape indices
.
For simplicity we will often omit tape indices ![]() .
Each tape has:
.
Each tape has: