We assume an initial set of user-defined primitive behaviors reflecting prior knowledge and assumptions of the user. Primitives may be assembler-like instructions or time-consuming software, such as, say, theorem provers, or matrix operators for neural network-like parallel architectures, or trajectory generators for robot simulations, or state update procedures for multiagent systems, etc. Each primitive is represented by a token in Q. It is essential that those primitives whose runtimes are not known in advance can be interrupted by OOPS at any time.
The searcher's initial bias is also affected by initial, user-defined, task-dependent probability distributions on the finite or infinite search space of possible self-delimiting program prefixes. In the simplest case we start with a maximum entropy distribution on the tokens, and define prefix probabilities as the products of the probabilities of their tokens. But prefix continuation probabilities may also depend on previous tokens in context sensitive fashion defined by a probabilistic syntax diagram. In fact, we even permit that any executed prefix assigns a task-dependent, self-computed probability distribution to its own possible suffixes (compare Section 3.1).
Consider the left-hand side of Figure 1.
All instruction pointers ![]() of all
current tasks
of all
current tasks ![]() are initialized by some address,
typically below the topmost code address,
thus accessing the code bias common to all tasks,
and/or using task-specific code fragments written
into tapes.
All tasks keep executing their instructions in parallel
until one of them is interrupted or all tasks are solved,
or until some task's instruction pointer points to the yet unused
address right after the
topmost code address. The latter case
is interpreted as a request for code prolongation through a new token,
where each token has a probability
according to the present task's current state-encoded
distribution on the possible next tokens.
The deterministic method Try systematically
examines all possible code extensions in a depth-first fashion
(probabilities of prefixes are just used to order them for runtime
allocation).
Interrupts and backtracking to previously selected tokens
(with yet untested alternatives) and the corresponding partial resets
of states and task sets
take place whenever one of the tasks encounters an error,
or the product of the task-dependent probabilities of the currently selected tokens
multiplied by the sum of the runtimes on all tasks exceeds a given
total search time limit
are initialized by some address,
typically below the topmost code address,
thus accessing the code bias common to all tasks,
and/or using task-specific code fragments written
into tapes.
All tasks keep executing their instructions in parallel
until one of them is interrupted or all tasks are solved,
or until some task's instruction pointer points to the yet unused
address right after the
topmost code address. The latter case
is interpreted as a request for code prolongation through a new token,
where each token has a probability
according to the present task's current state-encoded
distribution on the possible next tokens.
The deterministic method Try systematically
examines all possible code extensions in a depth-first fashion
(probabilities of prefixes are just used to order them for runtime
allocation).
Interrupts and backtracking to previously selected tokens
(with yet untested alternatives) and the corresponding partial resets
of states and task sets
take place whenever one of the tasks encounters an error,
or the product of the task-dependent probabilities of the currently selected tokens
multiplied by the sum of the runtimes on all tasks exceeds a given
total search time limit ![]() .
.
To allow for efficient backtracking, Try tracks effects of tested program prefixes, such as task-specific state modifications (including probability distribution changes) and partially solved task sets, to reset conditions for subsequent tests of alternative, yet untested prefix continuations in an optimally efficient fashion (at most as expensive as the prefix tests themselves).
Since programs are created online while they are being executed, Try will never create impossible programs that halt before all their tokens are read. No program that halts on a given task can be the prefix of another program halting on the same task. It is important to see, however, that in our setup a given prefix that has solved one task (to be removed from the current task set) may continue to demand tokens as it tries to solve other tasks.
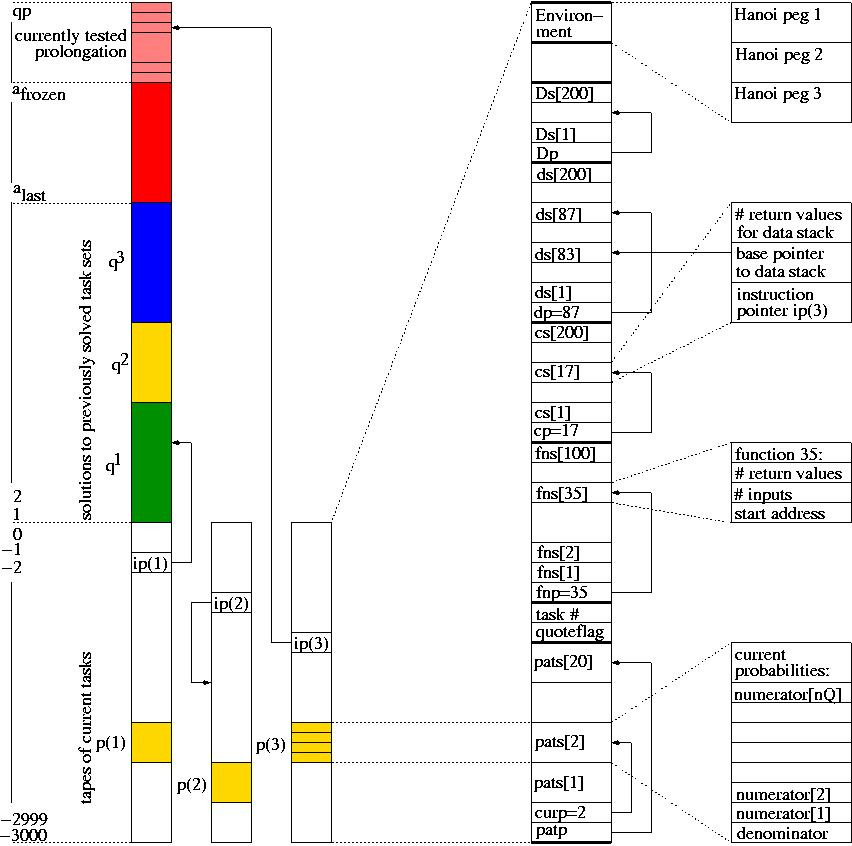 |
 Figure 2:
Search tree during an OOPS application; compare Section 4.1 and
Figure 1.
Search tree during an OOPS application. The tree branches are program prefixes. A single prefix may modify several task-specific tapes in parallel. Nodes represent primitive instructions; widths of connections between nodes stand for temporary, task-specific transition probabilities encoded (yellow) on the modifiable computation tapes (white, to the right; one tape per task; each tape has an instruction pointer). Prefixes may contain (or call previously frozen) subprograms that dynamically modify the conditional probabilities during runtime, thus rewriting the suffix search procedure. In the example, the currently tested prefix (pink, above the previously frozen codes) consists of the token sequence "while (x /< y) call fn17" (real values in the tree denote transition probabilities). Here fn17 might be a time-consuming instruction, say, for manipulating the arm of a realistic virtual robot. Before requesting an additional token, this prefix may run for a long time, thus changing many components of numerous tapes. Node-oriented backtracking will restore partially solved task sets and modifications of internal states and continuation probabilities once there is an error or the sum of the runtimes of the current prefix on all current tasks exceeds the prefix probability multiplied multiplied by the current search time limit, which keeps doubling until the current task set is solved.
See text for details.
Figure 2:
Search tree during an OOPS application; compare Section 4.1 and
Figure 1.
Search tree during an OOPS application. The tree branches are program prefixes. A single prefix may modify several task-specific tapes in parallel. Nodes represent primitive instructions; widths of connections between nodes stand for temporary, task-specific transition probabilities encoded (yellow) on the modifiable computation tapes (white, to the right; one tape per task; each tape has an instruction pointer). Prefixes may contain (or call previously frozen) subprograms that dynamically modify the conditional probabilities during runtime, thus rewriting the suffix search procedure. In the example, the currently tested prefix (pink, above the previously frozen codes) consists of the token sequence "while (x /< y) call fn17" (real values in the tree denote transition probabilities). Here fn17 might be a time-consuming instruction, say, for manipulating the arm of a realistic virtual robot. Before requesting an additional token, this prefix may run for a long time, thus changing many components of numerous tapes. Node-oriented backtracking will restore partially solved task sets and modifications of internal states and continuation probabilities once there is an error or the sum of the runtimes of the current prefix on all current tasks exceeds the prefix probability multiplied multiplied by the current search time limit, which keeps doubling until the current task set is solved.
See text for details.