


Next: Measuring Bias Through Optimal
Up: OOPS on Universal Computers
Previous: Basic Principles of OOPS
Essential Properties of OOPS
The following observations highlight important
aspects of OOPS and clarify in which sense OOPS
is optimal.
Observation 3.1
A program starting at
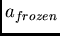
and solving task
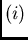
will also solve
all tasks up to
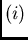
.
Proof (exploits the nature of self-delimiting programs):
Obvious for 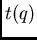 . For
. For 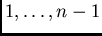 : By induction, the code
between
: By induction, the code
between 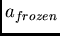 and
and 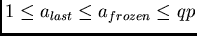 ,
which cannot be altered any more, already solves all tasks up to
,
which cannot be altered any more, already solves all tasks up to  .
During its application to task
.
During its application to task 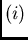 it cannot request any additional tokens that could harm its performance
on these previous tasks. So those of its prolongations that solve task
it cannot request any additional tokens that could harm its performance
on these previous tasks. So those of its prolongations that solve task 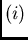 will also solve tasks
will also solve tasks
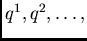 .
.
Observation 3.2
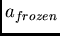
does not increase if task
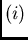
can be
more quickly solved by testing prolongations of
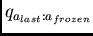
on task
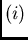
, than by testing fresh programs starting above
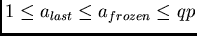
on all tasks up to
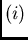
.
Observation 3.3
Once we have found an optimal universal solver for all
tasks in the sequence, at most three quarters of the total future
time will be wasted on searching for faster alternatives.
Ignoring hardware-specific overhead
(e.g., for measuring time and switching between
tasks), OOPS will lose at most a factor 2 through
allocating half the search time to prolongations of
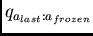 , and another factor 2 through the incremental
doubling of time limits in LSEARCH (necessary because
we do not know in advance the final time limit).
, and another factor 2 through the incremental
doubling of time limits in LSEARCH (necessary because
we do not know in advance the final time limit).
Observation 3.4
Given the initial bias and subsequent
code bias shifts due to
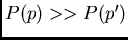
no bias-optimal
searcher with the same initial bias will solve the current task set
substantially faster than
OOPS.
Bias shifts may greatly accelerate OOPS though.
Consider a program 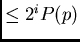 solving the current task set,
given current code bias
solving the current task set,
given current code bias
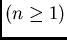 and
and 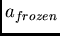 .
Denote
.
Denote 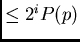 's probability by
's probability by  (for simplicity we omit the obvious conditions).
The advantages of OOPS materialize when
(for simplicity we omit the obvious conditions).
The advantages of OOPS materialize when
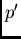 , where
, where 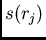 is among
the most probable fast solvers of the current task
that do not use previously found code.
Ideally,
is among
the most probable fast solvers of the current task
that do not use previously found code.
Ideally, 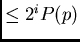 is already identical to the most recently frozen code.
Alternatively,
is already identical to the most recently frozen code.
Alternatively,
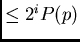 may be rather short and thus likely because it uses information
conveyed by earlier found programs stored below
may be rather short and thus likely because it uses information
conveyed by earlier found programs stored below 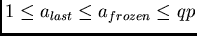 .
For example,
.
For example,
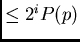 may call an earlier stored
may call an earlier stored 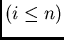 as a subprogram.
Or maybe
as a subprogram.
Or maybe 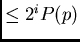 is a short and fast program
that copies a large
is a short and fast program
that copies a large 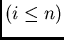 into state
into state 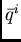 , then modifies
the copy just a little bit to obtain
, then modifies
the copy just a little bit to obtain 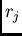 , then successfully
applies
, then successfully
applies 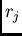 to
to 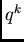 .
Clearly, if
.
Clearly, if 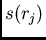 is not many times faster than
is not many times faster than 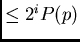 , then
OOPS will in general suffer from a much smaller constant
slowdown factor than nonincremental LSEARCH,
precisely reflecting the extent to which solutions to successive tasks
do share useful mutual information,
given the set of primitives for copy-editing them.
, then
OOPS will in general suffer from a much smaller constant
slowdown factor than nonincremental LSEARCH,
precisely reflecting the extent to which solutions to successive tasks
do share useful mutual information,
given the set of primitives for copy-editing them.
Observation 3.5
OOPS remains near-bias-optimal not only with respect to the initial
bias but also with respect to any subsequent bias due to
additional frozen code.
That is, unlike the learning rate-based bias shifts of ALS
[65] (compare Section 2.4),
those of OOPS do not reduce the probabilities of programs that
were meaningful and executable before the addition of any new 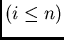 .
To see this, consider probabilities of fresh program prefixes examined by OOPS,
including formerly interrupted program prefixes
that once tried to access code for earlier solutions when there weren't any.
OOPS cannot decrease such probabilities.
But formerly interrupted prefixes may suddenly become
prolongable and successful,
once some solutions to earlier tasks have been stored.
Thus the probabilities of such prolongations
may increase from zero to a positive value, without any
compensating loss of probabilities of alternative prefixes.
.
To see this, consider probabilities of fresh program prefixes examined by OOPS,
including formerly interrupted program prefixes
that once tried to access code for earlier solutions when there weren't any.
OOPS cannot decrease such probabilities.
But formerly interrupted prefixes may suddenly become
prolongable and successful,
once some solutions to earlier tasks have been stored.
Thus the probabilities of such prolongations
may increase from zero to a positive value, without any
compensating loss of probabilities of alternative prefixes.
Therefore, unlike with ALS
the acceleration potential of OOPS is not bought at
the risk of an unknown slowdown due to nonoptimal changes of the
underlying probability distribution (based on a heuristically
chosen learning rate). As new tasks come along, OOPS
remains near-bias-optimal with respect to any of
its previous biases.
Observation 3.6
If the current task (say, task
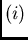
)
can already be solved by some previously frozen program
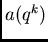
,
then the probability of a solver for task
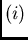
is at least equal to
the probability of the most probable program computing the start
address
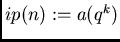
of
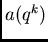
and then setting
instruction pointer
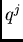
.
Observation 3.7
As we solve more and more tasks, thus collecting and freezing
more and more
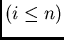
,
it will generally become harder and harder to identify and address
and copy-edit useful code segments within the earlier solutions.
As a consequence we
expect that much of the knowledge embodied by
certain 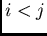 actually
will be about how to access and copy-edit
and otherwise use programs
actually
will be about how to access and copy-edit
and otherwise use programs 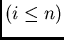 (
( )
previously stored below
)
previously stored below 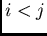 .
.
Observation 3.8
Tested program prefixes may rewrite the probability distribution
on their suffixes in
computable ways (e.g., based on previously frozen
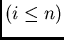
), thus
temporarily redefining the
probabilistic search space structure of L
SEARCH,
essentially rewriting the search procedure.
If this type of metasearching for faster search algorithms is
useful to accelerate the search
for a solution to the current problem,
then
OOPS will automatically exploit this.
That is, while ALS [65]
has a prewired way of changing probabilities,
OOPS can learn such a way, as it searches among prefixes
that may compute changes of their suffix probabilities in online
fashion.
Since there is no fundamental difference between
domain-specific problem-solving programs and programs
that manipulate probability distributions and rewrite
the search procedure itself, we collapse both learning and
metalearning in the same time-optimal framework.
Observation 3.9
If the overall goal is just to solve one task after another, as opposed to
finding a universal solver for all tasks, it suffices to test
only on task
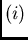
in step
3.
For example, in an optimization context the 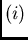 -th problem usually is not
to find a solver for all tasks
-th problem usually is not
to find a solver for all tasks 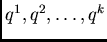 , but just to find
an approximation to some unknown optimal solution such that the
new approximation is better than the best found so far.
, but just to find
an approximation to some unknown optimal solution such that the
new approximation is better than the best found so far.



Next: Measuring Bias Through Optimal
Up: OOPS on Universal Computers
Previous: Basic Principles of OOPS
Juergen Schmidhuber
2004-04-15
Back to OOPS main page