OOPS Publications:
1. J. Schmidhuber.
Optimal Ordered Problem Solver.
Machine Learning, 54, 211-254, 2004.
PDF.
HTML.
2.
Schmidhuber, J., Zhumatiy, V. and Gagliolo, M. Bias-Optimal
Incremental Learning of Control Sequences for Virtual Robots. In Groen,
F., Amato, N., Bonarini, A., Yoshida, E., and Kröse, B., editors:
Proceedings of the 8-th conference
on Intelligent Autonomous Systems, IAS-8, Amsterdam,
The Netherlands, pp. 658-665, 2004.
PDF .
3. J. Schmidhuber.
Bias-Optimal Incremental Problem Solving.
In S. Becker, S. Thrun, K. Obermayer, eds.,
Advances in Neural Information Processing Systems 15, NIPS'15,
MIT Press, Cambridge MA, p. 1571-1578, 2003.
PS.
PDF.
HTML.
4. Preprint:
TR IDSIA-12-02, 31 July 2002.
PS.GZ,
PDF,
arXiv.
Revised version 2.0 (Dec 23, 2002):
PS.GZ.
PDF.
|
|
|
MLJ 2004 abstract:
We introduce a general and in a certain sense
time-optimal way of solving one problem after another, efficiently
searching the space of programs that compute solution candidates,
including those programs that organize and manage and adapt
and reuse earlier acquired knowledge.
The Optimal Ordered Problem Solver OOPS
draws inspiration from Universal Search designed
for single problems and universal Turing machines.
It spends part of the total search time for a new problem on
testing programs that exploit previous solution-computing programs
in computable ways.
If the new problem can be solved faster by copy-editing/invoking previous
code than by solving the new problem from scratch, then OOPS
will find this out. If not, then at least the
previous solutions will not cause much harm.
We introduce an efficient, recursive, backtracking-based way of
implementing OOPS on realistic computers
with limited storage. Experiments
illustrate how OOPS can greatly profit from metalearning or
metasearching, that is, searching for faster search procedures.
Keywords: OOPS, bias-optimality, incremental optimal universal search,
metasearching & metalearning & self-improvement ,
hierarchical learning & subgoal generation.
(Has little to do with
Genetic Programming.)
|
|
|
NIPS 2003 abstract:
Given is a problem sequence and a probability distribution
(the bias) on programs computing solution candidates.
We present an optimally fast way of incrementally solving
each task in the sequence.
Bias shifts are computed by program prefixes that
modify the distribution on their suffixes by
reusing successful code for previous tasks
(stored in non-modifiable memory).
No tested program gets more
runtime than its probability times the total search time.
In illustrative experiments, ours becomes the first general system to
learn a universal solver for arbitrary n disk
Towers of Hanoi tasks (minimal solution size 2^n-1).
It demonstrates the advantages of incremental learning by
profiting from previously solved, simpler tasks involving
samples of a simple context free language.
|
|
. |
|
OOPS does have limitations.
For example, it is not directly
applicable in lifelong
reinforcement learning
scenarios
where the goal is to maximize
future expected reward
(here the evaluation of some
solution candidate would consume
the rest of the life).
However, we may use OOPS
to perform bias-optimal
proof search for the more
recent
Gödel machine,
which makes provably optimal self-improvements
in such general environments.
Earlier related work:
Universal search
and the "fastest" algorithm for all well-defined problems
Metalearning (learning to learn)
Speed Prior (a probability
distribution based on the fastest way of computing things)
(German home)
|
|
|
Extended abstract (from MLJ paper):
OOPS solves
one task after another, always optimally exploiting solutions to
earlier tasks when possible. It can be used for increasingly hard
problems of optimization or prediction. The initial bias is given
in form of a probability distribution P on programs for a universal
computer. An asymptotically fastest way of solving a single
given task is
non-incremental universal search
(Levin, 1973, 1984): In the i-th phase
(i=1,2,3...) test all programs p with runtime at most 2^iP(p) until the
task is solved. Now suppose there is an ordered sequence of tasks, e.g.,
the n-th task is to find a path through a maze that is shorter than the
best found so far. To reduce the search time for new tasks,
previous incremental extensions
of universal search tried to modify P through
experience with earlier tasks - but in a heuristic and non-general and
suboptimal way prone to overfitting.
OOPS, however, does it right. It is searching in the space of
self-delimiting programs that are immediately executed while being
generated, growing by one instruction whenever they request this.
To solve the n-th task we sacrifice half the total search time for
testing (through a variant of universal search) programs that have the
most recent successful program as a prefix. The other half remains for
testing fresh programs with arbitrary beginnings. When we are searching
for a universal solver for all tasks in the sequence we have to time-share
the second half (but not the first!) among all tasks 1...n.
Storage for the first found program computing a solution to the current
task becomes non-writeable. Programs tested during search for solutions
to later tasks may copy non-writeable code into separate modifiable
storage, to edit it and execute the modified result. Prefixes may also
recompute the probability distribution on their suffixes in arbitrary
computable ways, thus rewriting the search procedure on the suffixes.
This allows for metalearning or metasearching, that is, searching for
faster search procedures.
For realistic limited computers we need efficient backtracking in program
space to reset P-modifications and other storage contents modified by
tested programs. We introduce a recursive procedure for doing this in
near-optimal fashion: the method is essentially only 8 times slower than
the theoretically optimal one (which never assigns to any program a testing
time exceeding the program's probability times the total search time).
OOPS can solve tasks unsolvable by traditional reinforcement learners and
AI planners, such as Towers of Hanoi with 30 disks (minimal solution size
exceeds 10^9). In our experiments OOPS demonstrates incremental learning
by reusing previous solutions to discover a prefix that temporarily
rewrites the distribution on its suffixes, such that universal search
is accelerated by a factor of 1000. This illustrates the benefits of
self-improvement and metasearching.
We also outline OOPS-based reinforcement learners and
examine the physical limitations of OOPS.
|
|






|
|
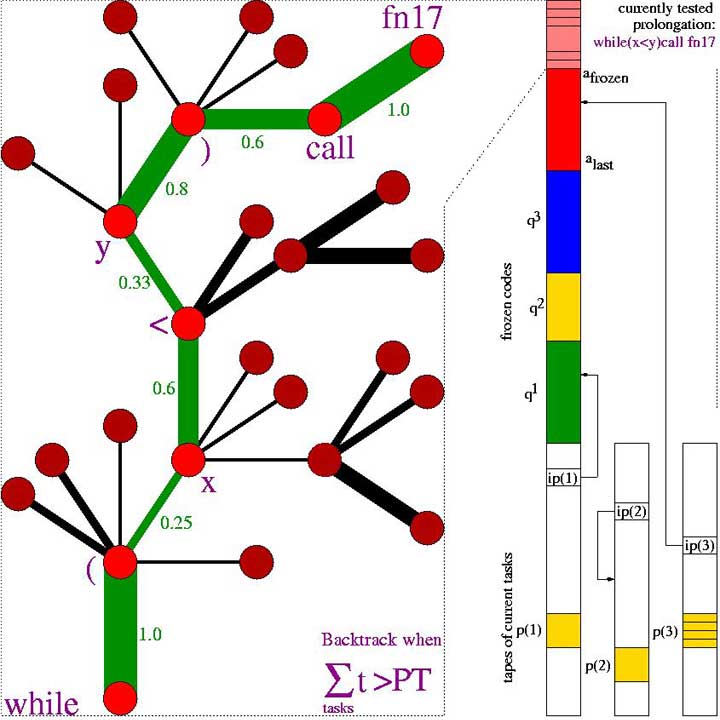
Search tree during an OOPS application.
The tree branches are program prefixes. A single prefix may modify several
task-specific tapes in parallel.
Nodes represent primitive instructions; widths of connections between
nodes stand for temporary, task-specific transition
probabilities encoded (yellow) on the modifiable computation tapes (white,
to the right; one tape per task; each tape has an instruction
pointer). Prefixes
may contain (or call previously frozen)
subprograms that dynamically modify the conditional
probabilities during runtime, thus rewriting the suffix search procedure.
In the example, the currently tested prefix (pink, above the previously frozen codes)
consists of the token sequence "while (x /< y) call fn17"
(real values in the tree denote transition probabilities).
Here fn17 might be a time-consuming instruction, say,
for manipulating the arm of a realistic virtual robot.
Before requesting an additional token, this prefix may run
for a long time, thus changing many components of numerous tapes.
Node-oriented backtracking will restore partially solved task sets and
modifications of internal states and continuation probabilities
once there is an error or the sum of the runtimes of the current
prefix on all current tasks exceeds the prefix probability
multiplied by the current search time limit, which
keeps doubling until the current task set is solved.
See paper for details.
|
|