Simple basis functions (BFs).
A BF is the function determining the activation of a code
component in response to a given input. Minimizing
![]() 's term
's term
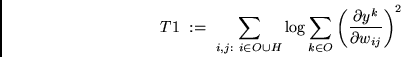
Sparseness.
Because ![]() tends to make
unit activations decrease to zero it favors sparse codes.
But
tends to make
unit activations decrease to zero it favors sparse codes.
But ![]() also favors a sparse hidden layer in the sense
that few hidden units contribute to producing the output.
also favors a sparse hidden layer in the sense
that few hidden units contribute to producing the output.
![]() 's second term
's second term
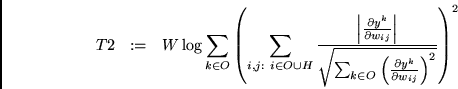
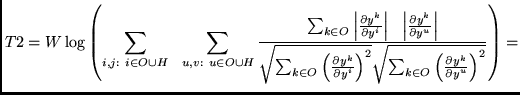 |
|||
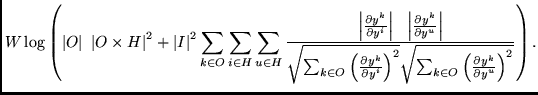 |
Few separated basis functions.
Hence FMS tries to figure out a way of using
(1) as few BFs
as possible for determining the activation of
each output unit,
while simultaneously (2) using the same BFs for
determining the activations of as many output
units as possible (common BFs).
(1) and ![]() separate the BFs:
the force towards simplicity (see
separate the BFs:
the force towards simplicity (see ![]() ) prevents
input information from being channelled through
a single BF; the force towards few
BFs per output makes them non-redundant.
(1) and (2) cause few BFs to determine all outputs.
) prevents
input information from being channelled through
a single BF; the force towards few
BFs per output makes them non-redundant.
(1) and (2) cause few BFs to determine all outputs.
Summary.
Collectively ![]() and
and ![]() (which make up
(which make up ![]() )
encourage sparse codes based on
few separated simple basis functions
producing all outputs.
Due to space limitations a more detailed analysis
(e.g. linear output activation) had to be left to
a TR [15] (on the WWW).
)
encourage sparse codes based on
few separated simple basis functions
producing all outputs.
Due to space limitations a more detailed analysis
(e.g. linear output activation) had to be left to
a TR [15] (on the WWW).