


Next: Bibliography
Up: SIMPLIFYING NEURAL NETS BY
Previous: A.2. HOW TO FLATTEN
Hinton and van Camp
[3]
minimize the sum of
two terms:
the first is conventional error plus variance, the other
is the distance
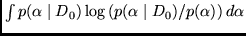 between
posterior
between
posterior
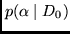 and prior
and prior 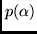 .
The problem is
to choose a ``good'' prior.
In contrast to their approach, our approach
does not require a ``good'' prior given in advance.
Furthermore, Hinton and van Camp
have to compute variances of weights and units,
which (in general) cannot be done using linear approximation.
Intuitively speaking, their weight variances are related to our
.
The problem is
to choose a ``good'' prior.
In contrast to their approach, our approach
does not require a ``good'' prior given in advance.
Furthermore, Hinton and van Camp
have to compute variances of weights and units,
which (in general) cannot be done using linear approximation.
Intuitively speaking, their weight variances are related to our
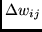 .
Our approach, however, does justify linear approximation.
.
Our approach, however, does justify linear approximation.
Juergen Schmidhuber
2003-02-25
Back to Financial Forecasting page