In a sense, searching is less general than reinforcement learning because it does not necessarily involve predictions of unseen data. Still, search is a central aspect of computer science (and any reinforcement learner needs a searcher as a submodule--see Section 10). Surprisingly, however, many books on search algorithms do not even mention the following, very simple asymptotically optimal, ``universal'' algorithm for a broad class of search problems.
Define a probability distribution ![]() on a finite or infinite
set of programs for a given computer.
on a finite or infinite
set of programs for a given computer. ![]() represents the searcher's
initial bias (e.g.,
represents the searcher's
initial bias (e.g., ![]() could be based on program length, or on a
probabilistic syntax diagram).
could be based on program length, or on a
probabilistic syntax diagram).
Method LSEARCH: Set current time limit T=1. WHILE problem not solved DO:LSEARCH (for Levin Search) may be the algorithm Levin was referring to in his 2 page paper [29] which states that there is an asymptotically optimal universal search method for problems with easily verifiable solutions, that is, solutions whose validity can be quickly tested. Given some problem class, if some unknown optimal programTest all programssuch that
, the maximal time spent on creating and running and testing
, satisfies
. Set
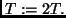
Recently Hutter
developed a more complex asymptotically
optimal search algorithm for all well-defined problems, not
just those with with easily verifiable solutions [23].
HSEARCH cleverly allocates part of the total
search time for searching the space of proofs to find provably correct
candidate programs with provable upper runtime bounds, and
at any given time
focuses resources on those programs with the currently
best proven time bounds.
Unexpectedly, HSEARCH manages to reduce
the unknown constant slowdown factor of LSEARCH to
a value of ![]() , where
, where ![]() is an
arbitrary positive constant.
is an
arbitrary positive constant.
Unfortunately, however, the search in proof space introduces an unknown additive problem class-specific constant slowdown, which again may be huge. While additive constants generally are preferrable over multiplicative ones, both types may make universal search methods practically infeasible.
HSEARCH and LSEARCH are nonincremental in the sense that
they do not attempt to minimize their constants by exploiting
experience collected in previous searches.
Our method
Adaptive LSEARCH or ALS
tries to overcome this
[57] -- compare Solomonoff's related ideas
[61,62].
Essentially it works as follows: whenever LSEARCH
finds a program ![]() that computes a solution for the current problem,
that computes a solution for the current problem,
![]() 's probability
's probability ![]() is
substantially increased using a ``learning rate,''
while probabilities of alternative programs decrease
appropriately.
Subsequent LSEARCHes for new problems then use the adjusted
is
substantially increased using a ``learning rate,''
while probabilities of alternative programs decrease
appropriately.
Subsequent LSEARCHes for new problems then use the adjusted
![]() , etc. A nonuniversal variant of this approach
was able to solve reinforcement learning (RL) tasks
[27]
in partially observable environments
unsolvable by traditional RL
algorithms [71,57].
, etc. A nonuniversal variant of this approach
was able to solve reinforcement learning (RL) tasks
[27]
in partially observable environments
unsolvable by traditional RL
algorithms [71,57].
Each LSEARCH invoked by ALS is optimal with respect to
the most recent adjustment of ![]() .
On the other hand, the modifications of
.
On the other hand, the modifications of ![]() themselves
are not necessarily optimal. Recent work discussed in the next section
overcomes this drawback in a principled way.
themselves
are not necessarily optimal. Recent work discussed in the next section
overcomes this drawback in a principled way.