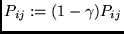LS is not necessarily optimal for ``incremental'' learning problems where
experience with previous problems may help to reduce future search costs.
To make an incremental search method out of non-incremental LS, we
introduce a simple, heuristic, adaptive LS extension (ALS) that uses
experience with previous problems to adaptively modify LS' underlying
probability distribution. ALS essentially works as follows: whenever LS
found a program ![]() that computed a solution for the current problem,
the probabilities of
that computed a solution for the current problem,
the probabilities of ![]() 's instructions
's instructions
![]() are increased (here
are increased (here
![]() denotes
denotes ![]() 's
's
![]() -th instruction, and
-th instruction, and ![]() denotes
denotes ![]() 's length -- if LS did not
find a solution (
's length -- if LS did not
find a solution (![]() is the empty program), then
is the empty program), then ![]() is defined
to be 0). This will increase the probability of the entire program.
The probability adjustment is controlled by a learning rate
is defined
to be 0). This will increase the probability of the entire program.
The probability adjustment is controlled by a learning rate ![]() (
(![]()
![]() ). ALS is related to the linear
reward-inaction algorithm, e.g., [#!Narendra:74!#,#!Kaelbling:93!#] -- the
main difference is: ALS uses LS to search through program space
as opposed to single action space. As in the previous section, the
probability distribution
). ALS is related to the linear
reward-inaction algorithm, e.g., [#!Narendra:74!#,#!Kaelbling:93!#] -- the
main difference is: ALS uses LS to search through program space
as opposed to single action space. As in the previous section, the
probability distribution ![]() is determined by
is determined by ![]() . Initially, all
. Initially, all
![]() . However, given a sequence of problems
. However, given a sequence of problems
![]() , the
, the ![]() may undergo changes caused by ALS:
may undergo changes caused by ALS:
ALS (problems
![]() , variable matrix
, variable matrix ![]() )
)
for:= 1 to
do:
:= Levin search(
,
); Adapt(
,
).
Adapt(program ![]() , variable matrix
, variable matrix ![]() )
)
for:= 1 to
,
:= 1 to
do:
if (=
) then
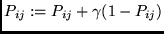
else