First term of
Simple component functions (CFs).
The term
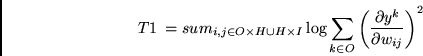
| (1) | |||
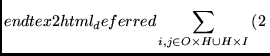 |
(2) | ||
| (3) | |||
| (4) | |||
| (5) | |||
| (6) | |||
| (7) | |||
 |
(8) | ||
| (9) | |||
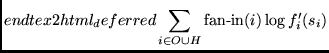 |
(10) | ||
| (11) | |||
| (12) | |||
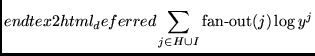 |
(13) | ||
| (14) | |||
| (15) | |||
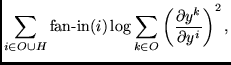 |
![]() makes
(1) unit activations decrease to zero
in proportion to their fan-outs, (2) first-order derivatives of activation
functions decrease to zero in proportion to their fan-ins, and (3) the
influence of units on the output decrease to zero in proportion to the
unit's fan-in. For a detailed analysis see Hochreiter and Schmidhuber (1997a).
makes
(1) unit activations decrease to zero
in proportion to their fan-outs, (2) first-order derivatives of activation
functions decrease to zero in proportion to their fan-ins, and (3) the
influence of units on the output decrease to zero in proportion to the
unit's fan-in. For a detailed analysis see Hochreiter and Schmidhuber (1997a).
![]() is the reason why low-complexity (or simple) CFs are
preferred.
is the reason why low-complexity (or simple) CFs are
preferred.
Sparseness.
Point (1) above favors sparse hidden unit activations
(here: few active components);
point (2)
favors non-informative hidden unit activations
hardly affected by small input changes.
Point (3) favors sparse hidden unit activations in the sense
that ``few hidden units contribute to producing the output''.
In particular, sigmoid hidden units
with activation function
![]() favor near-zero activations.
favor near-zero activations.