


Next: Infinite Computations, Convergence, Formal
Up: Preliminaries
Previous: Notation
The standard model of theoretical computer science is the Turing Machine
(TM) [43]. It allows for emulating any known computer. Most
TMs considered in previous work are monotone, that is, once they
print out a bit they cannot revise it later. We will point out that such
TMs are in a certain sense less expressive than other TMs that may edit
their previous outputs -- certain objects without any short nonhalting
programs on traditional TMs have very short programs on other TMs. To deal
with the differences between monotone computability, enumerability, and
computability in the limit, we consider three types of TMs.
Monotone TMs (MTMs). Most current theory of description
size and inductive inference is based on MTMs (compare [30, p. 276
ff]) with several tapes, each tape being a finite chain
of adjacent squares with a scanning head initially pointing to the
leftmost square. There is one output tape and at least two work tapes
(sufficient to efficiently compute everything traditionally regarded
as computable). The MTM has a finite number of internal states, one
of them being the initial state. MTM behavior is specified by a lookup
table mapping current state and contents of the squares above work tape
scanning heads to a new state and an instruction to be executed next.
There are instructions for shifting work tape scanning heads one square
left or right (appending new squares when necessary), and for writing 0
or 1 on squares above work tape scanning heads. The only input-related
instruction requests an input bit determined by an external process
and copies it onto the square above the first work tape scanning head
(no extra input tape). There may or may not be a halt instruction to
terminate a computation. MTMs are called monotone because they
have a one-way write-only output tape -- they cannot edit their previous
output, because the only ouput instructions are: append new square at
the right end of the output tape and fill it with 0/1.
General TMs (GTMs). GTMs embody the concept of computability in
the limit. They are like MTMs but have additional output instructions
to edit their previous output. Our motivation for introducing GTMs is
that certain bitstrings are very compactly describable on nonhalting
GTMs but not on MTMs, as will be seen later. This has consequences for
definitions of individual describability and probability distributions on
describable things. The additional instructions are: (a) shift output
scanning head right/left (but not out of bounds); (b) delete square
at the right end of the output tape (if it is not the initial square
or above the scanning head); (c) write 1 or 0 on square above output
scanning head. Compare Burgin's inductive TMs and super-recursive
algorithms [6,8].
Example.[Pseudorandom universe based on halting problem]
Why
consider GTMs at all? Because in a certain sense they represent the
non-plus-ultra of constructive computability. For instance, consider
a programmer of virtual realities. Which are his fundamental limits;
which universes could he possibly generate? He could write a finite
program that computes a never-ending sequence 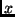 of finite bitstrings
of finite bitstrings
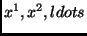 representing the history of some discrete universe,
where
representing the history of some discrete universe,
where 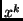 represents the state at discrete time step
represents the state at discrete time step 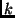 , and
, and 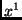 the ``Big Bang'' [35]. ``Noise'' will have to be
simulated by invoking a finite pseudorandom generator subroutine PRG.
Suppose its
the ``Big Bang'' [35]. ``Noise'' will have to be
simulated by invoking a finite pseudorandom generator subroutine PRG.
Suppose its 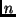 -th output bit
-th output bit 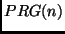 is 1 if the
is 1 if the 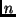 -th program of a
list of all possible programs halts, and 0 otherwise. There is no halting
algorithm computing
-th program of a
list of all possible programs halts, and 0 otherwise. There is no halting
algorithm computing 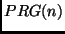 for all
for all 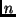 , otherwise the halting problem
would be solvable, which it is not [43]. Hence in general
there is no computer that outputs
, otherwise the halting problem
would be solvable, which it is not [43]. Hence in general
there is no computer that outputs 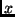 and only
and only 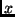 without ever
editing some previously computed history. That is, if we want to study
the set of all programmable universes [36] then we
should not limit ourselves to MTMs but consider GTMs as well.
without ever
editing some previously computed history. That is, if we want to study
the set of all programmable universes [36] then we
should not limit ourselves to MTMs but consider GTMs as well.
Note, however, that the output of
a GTM might not stabilize in the sense that certain output bits
might flip from 0 to 1 and back forever.
Enumerable Output Machines (EOMs). EOMs embody the important
concept of computable enumerability. Like GTMs, EOMs can edit their
previous output, but not such that it decreases lexicographically.
The expressive power of EOMs lies in between those of MTMs and GTMs, with
interesting universality properties whose analogues do not hold for GTMs.
EOMs are like MTMs, except that the only permitted output instruction
sequences are: (a) shift output tape scanning head left/right unless
this leads out of bounds; (b) replace bitstring starting above the
output scanning head by the string to the right of the scanning head
of the second work tape, readjusting output tape size accordingly, but
only if this lexicographically increases the contents of the output tape.
The necessary test can be hardwired into the finite TM transition table. A
significant fraction of this paper concerns EOMs with randomly chosen
input bits.
Self-Delimiting Programs.
Sequences of input bits requested by halting TMs
are traditionally called self-delimiting programs because they convey all
information about their own length [29,16,14].
Here we will use this term also for complete finite input sequences
requested by nonhalting MTMs, EOMs, and GTMs. Consider three possible cases:
(1) the input sequence is a halting self-delimiting program (traditional case),
(2) the TM at some point ceases requesting new input bits but does not halt
-- then we have a nonhalting self-delimiting program, which
may produce either finite or infinite output,
(3) the TM never ceases requesting new input bits,
which suggests the notion of infinite programs.
In any case no program can be prefix of another one.
Example. [Illustration of TM Hierarchy]
There are short self-delimiting MTM programs for the infinite
dyadic expansion of 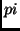 ,
but not for
,
but not for 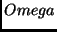 , the halting probability of an MTM
whose input bits are obtained by tossing an unbiased coin whenever it
requests a new bit
[14,10,39,9,42].
On the other hand,
there are short self-delimiting EOM programs for
, the halting probability of an MTM
whose input bits are obtained by tossing an unbiased coin whenever it
requests a new bit
[14,10,39,9,42].
On the other hand,
there are short self-delimiting EOM programs for 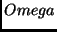 ,
but not for certain bitstrings
that have short self-delimiting GTM programs,
to be exhibited by Theorem 3.3.
,
but not for certain bitstrings
that have short self-delimiting GTM programs,
to be exhibited by Theorem 3.3.



Next: Infinite Computations, Convergence, Formal
Up: Preliminaries
Previous: Notation
Juergen Schmidhuber
2003-02-13