| (17) |
The traditional universal enumerable measure [40,45,29,16,17,41,14,30] studied in the theory of optimal inductive inference [40,41,24,23] reflects properties of a universal MTM with random input. In what follows we will simply replace the MTM by a more expressive EOM and obtain a nonenumerable measure that (1) dominates the traditional measure, (2) is ``just as computable'' in the limit as the traditional one, (3) is universal in its class. It will turn out though that this approach does not generalize to the case of GTMs. Some new definitions are in order.
| (17) |
Then
Proof. We first show that one can enumerate the CEMs, then construct a universal CEM from the enumeration. Check out the differences to Levin's proofs that there is a universal discrete semimeasure and a universal c.e. semimeasure [45,28], and Li and Vitányi's presentation of the latter [30, p. 273 ff], attributed to J. Tyszkiewicz.
Without loss of generality, consider only EOMs without
halt instruction and with fixed input
encoding of ![]() according to
Def. 2.8.
Such EOMs are c.e., and correspond
to an effective enumeration of all c.e. functions from
according to
Def. 2.8.
Such EOMs are c.e., and correspond
to an effective enumeration of all c.e. functions from ![]() to
to
![]() . Let
. Let ![]() denote the
denote the ![]() -th EOM in the list, and let
-th EOM in the list, and let
![]() denote its output
after
denote its output
after ![]() instructions when applied to
instructions when applied to ![]() .
The following procedure filters out those
.
The following procedure filters out those ![]() that already represent
CEMs, and transforms the others into representations
of CEMs, such that we obtain a way of generating all and only CEMs.
that already represent
CEMs, and transforms the others into representations
of CEMs, such that we obtain a way of generating all and only CEMs.
FOR allDO in dovetail fashion:
START: letand
and
denote variable functions on
. Set
, and
for all other
. Define
for undefined
. Let
denote a string variable.
FORDO:
(1) Lexicographically order and rename allwith
:
.
(2) FORdown to 1 DO:
(2.1) Systematically search for the smallestsuch that
AND
if
; set
.
(3) For allsatisfying
, set
. For all
with
, set
. For all
with
, set
.
If ![]() indeed represents a CEM
indeed represents a CEM ![]() then
each search process in (2.1) will terminate, and
the
then
each search process in (2.1) will terminate, and
the ![]() will enumerate the
will enumerate the
![]() from below, and
the
from below, and
the ![]() and
and
![]() will approximate the true
will approximate the true ![]() and
and
![]() , respectively,
not necessarily from below though.
Otherwise there will be a nonterminating search
at some point, leaving
, respectively,
not necessarily from below though.
Otherwise there will be a nonterminating search
at some point, leaving ![]() from the previous loop
as a trivial CEM. Hence we can enumerate all CEMs,
and only those. Now define (compare [28]):
from the previous loop
as a trivial CEM. Hence we can enumerate all CEMs,
and only those. Now define (compare [28]):
| (19) |
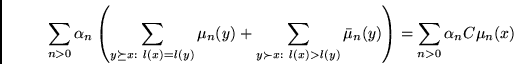 |
(20) |