


Next: Dominant and Universal (Semi)Measures
Up: HIERARCHIES OF GENERALIZED KOLMOGOROV
Previous: Relation to Conditional Complexity
Measures and Probability Distributions
We will now show how the Kolmogorov complexity hierarchy introduced
above translates into an algorithmic prior hierarchy.
Suppose 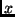 represents the history of our universe up until now.
What is its most likely continuation
represents the history of our universe up until now.
What is its most likely continuation
 ? Bayes' theorem yields
? Bayes' theorem yields
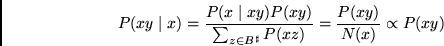 |
(13) |
where
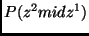 is the probability
of
is the probability
of 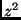 , given knowledge of
, given knowledge of 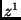 , and
, and
 |
(14) |
is a normalizing factor.
The most likely continuation 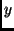 is
determined by
is
determined by 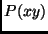 , the prior probability of
, the prior probability of 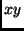 .
Now what are the formally describable ways of assigning prior probabilities
to computable universes?
In what follows we will first consider traditional
describable semimeasures on
.
Now what are the formally describable ways of assigning prior probabilities
to computable universes?
In what follows we will first consider traditional
describable semimeasures on 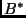 ,
then nontraditional probability distributions on
,
then nontraditional probability distributions on 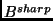 .
.
Subsections
Juergen Schmidhuber
2003-02-13
![]() represents the history of our universe up until now.
What is its most likely continuation
represents the history of our universe up until now.
What is its most likely continuation
![]() ? Bayes' theorem yields
? Bayes' theorem yields