BASIC CONCEPTS

Each Turing machine (TM) $C$ (mapping bitstrings to bitstrings, without loss of generality) computes a partial function $f_C: \{0,1\}^* \rightarrow \{0,1\}^*$ ($f_C$ is undefined where $C$ does not halt). The Kolmogorov complexity $K_U(s)$ of a finite string $s$ is the length of the shortest program $p$ that computes $s$ on a universal Turing machine $U$ and halts, where the set of possible halting programs forms a prefix code (no halting program can be the prefix of another one):

$$K_U(s) = \min_p\{\mid p \mid : ~f_U(p) = s \},$$

where $\mid p \mid$ denotes the length of $p$. The invariance theorem (Solomonoff, 1964; Kolmogorov, 1965; Chaitin, 1969) states that $K_{U_1}(s) = K_{U_2}(s) + O(1)$ for two universal machines $U_1$ and $U_2$ and for all $s$. Therefore we may drop the index $U$ and write $K$ instead of $K_U$.

Machine learning and the prior problem. In machine learning applications, we are often concerned with the following problem: given training data $D$, we would like to select the most probable hypothesis $H$ generating the data. Bayes formula yields

$$P(H \mid D) = \frac{ P(D \mid H) P(H) }{ P(D)}.$$ (1)

We would like to select $H$ such that $P(H \mid D)$ is maximal. Taking the log of this equation leads to the principle of minimum description length (Wallace, 1968; Rissanen, 1978). But where does the prior $P(H)$ come from? How does one define an a priori probability distribution on the set of possible hypotheses without introducing arbitrariness? This is often perceived as the prior problem of Bayesian approaches. The theory of algorithmic probability, however, provides a solution, as will be seen next.

Universal prior (Levin, 1974; Solomonoff, 1964; Gacs, 1974; Chaitin, 1975). Define $P_U(s)$, the a priori probability of a bitstring $s$, as the probability of guessing a halting program that computes $s$ on universal TM $U$. Here, the way of guessing is defined by the following procedure: whenever the scanning head of $U$'s input tape (initially blank) shifts right to a field that has not been scanned before, do: With probability $\frac{1}{2}$ fill it with a 0; with probability $\frac{1}{2}$ fill it with a 1. We obtain

$$P_U(s) = \sum_{p: f_U(p) = s} (\frac{1}{2})^{\mid p \mid}.$$

Under different universal priors (based on different universal machines), probabilities of a given string differ by not more than a constant factor independent of the string size, due to the invariance theorem. Therefore we may drop the index $U$ and write $P$ instead of $P_U$. This justifies the name ``universal prior'', also known as the Solomonoff-Levin distribution. Universal priors appear to be the only convincing method for assigning a priori probabilities to hypotheses (or other computable objects).

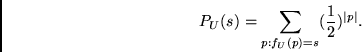
Dominance of shortest programs. It can be shown (Levin, 1974; Chaitin, 1975) that

$$P(s) = O(2^{-K(s)}).$$

The probability of a string is dominated by the probabilities of its shortest programs. This justifies ``Occam's razor'': in equation (1), the a priori most probable $H$ are those with minimal Kolmogorov complexity.

Dominance of universal prior. Suppose there are infinitely many enumerable solution candidates (strings): amazingly, $P_U$ dominates all discrete enumerable semimeasures P (including probability distributions, see e.g. Li and Vitanyi (1993) for details) in the following sense: for each $P$ there is a constant $c$ such that $P_U(s) >= cP(s)$ for all strings $s$.

Since Kolmogorov complexity is incomputable in general, the universal prior is so, too. A popular myth states that this fact renders useless the concepts of Kolmogorov complexity, as far as practical machine learning is concerned. But this is not so, as will be seen next. There we focus on a natural, computable, yet very general extension of Kolmogorov complexity.

Levin complexity. In what follows, a (not necessarily halting) program is a string on $U$'s input tape which can be scanned completely by $U$. Let $U$ scan a program $q$ before it finishes printing $s$ onto the work tape. Let $t(q, s)$ be the number of steps taken before $s$ is printed. Then

$$Kt(s) = \min_q\{\mid q \mid + log~t(q,s) \}.$$

An invariance theorem similar to the one for $K$ holds for $Kt$ as well.

Levin's universal optimal search algorithm (Levin, 1973; 1984). Suppose we are looking for the solution (a string) to a given problem. Levin's universal search algorithm generates and evaluates all strings (solution candidates) in order of their $Kt$ complexity, until a solution is found. This is essentially equivalent to enumerating all programs in order of decreasing probabilities, divided by their runtimes. Each program computes a string that is tested to see whether it is a solution to the given problem. If so, the search is stopped. Amazingly, for a broad class of problems, including inversion problems and time-limited optimization problems, universal search can be shown to be optimal with respect to total expected search time, leaving aside a constant factor independent of the problem size: if string $s$ can be computed within $t$ time steps by a program $p$, and the probability of guessing $p$ (as above) is $\bar{P}$, then within $O(\frac{t}{\bar{P}})$ time steps, systematic enumeration according to Levin will generate $p$, run it for $t$ time steps, and output $s$. In the experiments below, a probabilistic algorithm strongly inspired by universal search will be used.

Back to Optimal Universal Search page
Back to Program Evolution page
Back to Algorithmic Information page
Back to Speed Prior page