



Nächste Seite: On-Line VERSUS Off-Line
Aufwärts: DYNAMISCHE VERBINDUNGEN
Vorherige Seite: PERFORMANZMASS
Inhalt
Für alle Gewichte
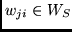 (vom Knoten
(vom Knoten  zum Knoten
zum Knoten 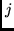 )
interessiert uns das Inkrement
)
interessiert uns das Inkrement
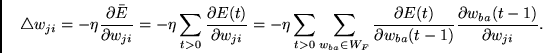 |
(3.6) |
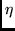 bezeichnet dabei eine konstante positive Lernrate.
bezeichnet dabei eine konstante positive Lernrate.
Zu jedem Zeitschritt 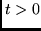 läßt sich der Faktor
läßt sich der Faktor
durch konventionelles BP bestimmen (siehe Kapitel 1).
Wir schreiben für Knoten 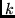 in
in 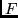 :
:
Falls 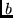 einen Ausgabeknoten bezeichnet, so ist
einen Ausgabeknoten bezeichnet, so ist
Steht 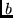 hingegen für einen versteckten Knoten der
hingegen für einen versteckten Knoten der 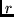 -ten Lage
von
-ten Lage
von 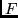 , so gilt
, so gilt
Für 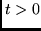 erhalten wir nun mit der Kettenregel die Rekursion
erhalten wir nun mit der Kettenregel die Rekursion
Wir verwenden eine durch den RTRL-Algorithmus
(siehe Kapitel 2) inspirierte Methode:
Für jedes
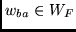 und jedes
und jedes
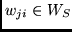 führen wir eine Variable
führen wir eine Variable
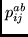 ein und initialisieren sie zu Beginn einer
Trainingssequenz mit 0.
ein und initialisieren sie zu Beginn einer
Trainingssequenz mit 0.
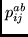 läßt sich zu jedem Zeitschritt
läßt sich zu jedem Zeitschritt
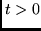 aktualisieren:
aktualisieren:
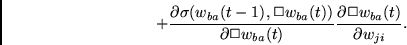 |
(3.7) |
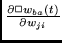 hängt davon ab, welche der beiden Architekturen wir
benutzen wollen.
Eine geeignete BP-Prozedur liefert uns jedenfalls
für jedes
hängt davon ab, welche der beiden Architekturen wir
benutzen wollen.
Eine geeignete BP-Prozedur liefert uns jedenfalls
für jedes
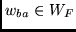 den Wert
den Wert
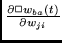 für alle
für alle
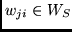 . Nach Aktualisierung der
. Nach Aktualisierung der 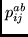 Variablen
wird (3.6)
mittels der Formel
Variablen
wird (3.6)
mittels der Formel
bestimmbar.
(3.4) und (3.5) unterscheiden sich lediglich in der Art und Weise, in
der Fehlersignale für 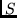 ' Ausgabeknoten berechnet werden:
Wird Architektur 1 verwendet, benützen wir konventionelles
BP zur Berechnung von
' Ausgabeknoten berechnet werden:
Wird Architektur 1 verwendet, benützen wir konventionelles
BP zur Berechnung von
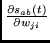 in (3.7). Dann
schreiben wir für Knoten
in (3.7). Dann
schreiben wir für Knoten 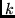 in
in 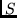 :
:
Bezeichnet 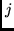 einen Ausgabeknoten (mit
einen Ausgabeknoten (mit 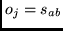 ), so gilt
), so gilt
Stellt 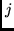 hingegen einen versteckten Knoten der
hingegen einen versteckten Knoten der 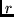 -ten Lage von
-ten Lage von 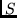 dar, so ist
dar, so ist
Bei Verwendung von Architektur 2 ist zu
berücksichtigen, daß
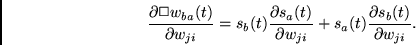 |
(3.8) |
Mit BP berechnet man am besten
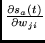 für jeden
Ausgabeknoten
für jeden
Ausgabeknoten 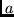 und für alle
und für alle 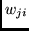 . Die Resultate
lassen sich in
. Die Resultate
lassen sich in
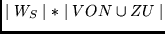 Variablen
unterbringen. Nun löst man Gleichung (3.7) in einem
zweiten Durchgang.
Variablen
unterbringen. Nun löst man Gleichung (3.7) in einem
zweiten Durchgang.
Bei beiden Architekturen beträgt
die Berechnungskomplexität pro Zeitschritt
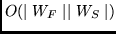 .
.
Unterabschnitte




Nächste Seite: On-Line VERSUS Off-Line
Aufwärts: DYNAMISCHE VERBINDUNGEN
Vorherige Seite: PERFORMANZMASS
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite
![]() (vom Knoten
(vom Knoten ![]() zum Knoten
zum Knoten ![]() )
interessiert uns das Inkrement
)
interessiert uns das Inkrement
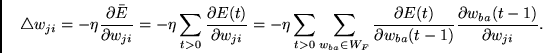
![]() läßt sich der Faktor
läßt sich der Faktor
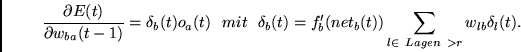
![]() erhalten wir nun mit der Kettenregel die Rekursion
erhalten wir nun mit der Kettenregel die Rekursion
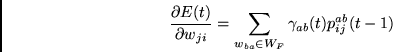
![]() ' Ausgabeknoten berechnet werden:
Wird Architektur 1 verwendet, benützen wir konventionelles
BP zur Berechnung von
' Ausgabeknoten berechnet werden:
Wird Architektur 1 verwendet, benützen wir konventionelles
BP zur Berechnung von
![]() in (3.7). Dann
schreiben wir für Knoten
in (3.7). Dann
schreiben wir für Knoten ![]() in
in ![]() :
:
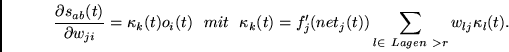
![]() für jeden
Ausgabeknoten
für jeden
Ausgabeknoten ![]() und für alle
und für alle ![]() . Die Resultate
lassen sich in
. Die Resultate
lassen sich in
![]() Variablen
unterbringen. Nun löst man Gleichung (3.7) in einem
zweiten Durchgang.
Variablen
unterbringen. Nun löst man Gleichung (3.7) in einem
zweiten Durchgang.
![]() .
.