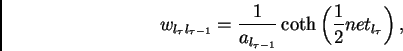Next: Weak upper bound for
Up: Exponential error decay
Previous: Error path integral
If
for all 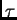 then the largest product increases exponentially with
then the largest product increases exponentially with 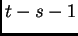 . That is,
the error blows up, and conflicting error signals arriving at unit
. That is,
the error blows up, and conflicting error signals arriving at unit 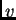 can lead to oscillating weights and unstable learning
(for error blow-ups or bifurcations
see also [19,2,8]).
On the other hand, if
can lead to oscillating weights and unstable learning
(for error blow-ups or bifurcations
see also [19,2,8]).
On the other hand, if
for all 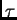 ,
then the largest product decreases exponentially with
,
then the largest product decreases exponentially with 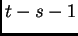 . That is,
the error vanishes, and nothing can be learned in acceptable time.
If
. That is,
the error vanishes, and nothing can be learned in acceptable time.
If 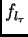 is the logistic
sigmoid function,
then the maximal value of
is the logistic
sigmoid function,
then the maximal value of 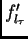 is 0.25.
If
is 0.25.
If
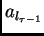 is constant and not equal to zero,
then the size of the gradient
is constant and not equal to zero,
then the size of the gradient
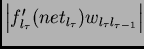 takes on maximal values
where
takes on maximal values
where
the size of the derivative goes to zero
for
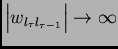 , and it
is less than
, and it
is less than  for
for
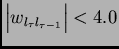 (e.g., if the absolute maximal weight value
(e.g., if the absolute maximal weight value 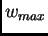 is smaller
than 4.0).
Hence with conventional logistic sigmoid transfer functions,
the error flow tends to vanish
as long as the weights have absolute values below 4.0,
especially in the beginning of the training phase.
In general the use of larger initial weights does not
help though -- as seen above,
for
is smaller
than 4.0).
Hence with conventional logistic sigmoid transfer functions,
the error flow tends to vanish
as long as the weights have absolute values below 4.0,
especially in the beginning of the training phase.
In general the use of larger initial weights does not
help though -- as seen above,
for
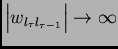 the relevant derivative goes to zero ``faster''
than the absolute weight can grow
(also, some weights may have to change their signs
by crossing zero).
Likewise, increasing the learning rate does not help either --
it does not change the ratio of
long-range error flow and short-range error flow.
BPTT is too sensitive to recent distractions.
Note that since the summation terms
in equation (2)
may have different signs,
increasing the number of units
the relevant derivative goes to zero ``faster''
than the absolute weight can grow
(also, some weights may have to change their signs
by crossing zero).
Likewise, increasing the learning rate does not help either --
it does not change the ratio of
long-range error flow and short-range error flow.
BPTT is too sensitive to recent distractions.
Note that since the summation terms
in equation (2)
may have different signs,
increasing the number of units 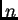 does not necessarily increase error flow.
does not necessarily increase error flow.



Next: Weak upper bound for
Up: Exponential error decay
Previous: Error path integral
Juergen Schmidhuber
2003-02-19