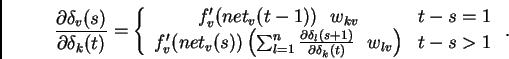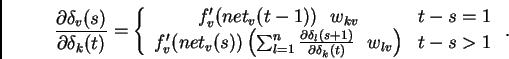Next: Intuitive explanation of equation
Up: Exponential error decay
Previous: Gradients of the error
Suppose we have a fully connected net
whose non-input unit indices range from 1 to 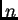 .
Let us focus on local error flow from output unit
.
Let us focus on local error flow from output unit 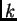 to
arbitrary unit
to
arbitrary unit 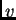 (later we will see that the analysis immediately
extends to global error flow).
The error occurring at
(later we will see that the analysis immediately
extends to global error flow).
The error occurring at 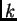 at time step
at time step 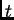 is propagated ``back in time''
for
is propagated ``back in time''
for 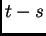 time steps,
to an arbitrary unit
time steps,
to an arbitrary unit 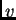 at time
at time 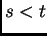 .
This scales the error by the following factor:
.
This scales the error by the following factor:
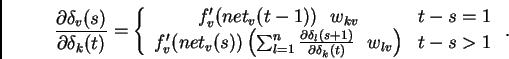 |
(1) |
In order to solve the above equation, we will expand it by unrolling
over time (as done for example in deriving BPTT). In particular, for
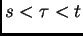 let
let 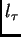 denote the index of a generic
non input unit in the replica of the network at time
denote the index of a generic
non input unit in the replica of the network at time 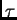 .
Moreover, let
.
Moreover, let 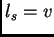 and
and 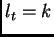 . We obtain:
. We obtain:
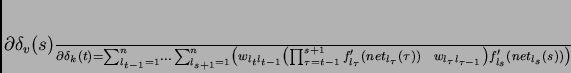 |
(2) |
(proof by induction).
It can be immediately shown that if the local error vanishes, then
the global error vanishes too. To see this compute
where 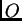 denotes the set of output units.
denotes the set of output units.



Next: Intuitive explanation of equation
Up: Exponential error decay
Previous: Gradients of the error
Juergen Schmidhuber
2003-02-19