


Next: Probabilistic target propagation
Up: Remedies
Previous: Ring's approach
The difficulty of learning long-term dependencies is strictly related
to the continuous optimization approach that guides the search for a
weight solution. One possibility for avoiding the problem is to resort
to other kinds of search in weight space, in which the operators for
generating another candidate weight solution are not based on continuous
gradients. Bengio et al. [6]
investigate methods such as simulated annealing,
multi-grid random search, and discrete error propagation.
Angeline et al. [1] (see also crossreference
Chapter 15) propose a genetic approach that also avoids gradient
computation.
The simplest kind of search without gradient, however,
simply randomly initializes all
network weights until the resulting net happens to classify
all training sequences correctly. In fact,
as discussed in crossreference Chapter 9 of this book,
simple weight guessing solves several popular
benchmarks described in previous work faster than the
recurrent net algorithms proposed therein
(compare [13]).
This does not mean that weight guessing is a good
algorithm. It just means that the problems are very simple.
More realistic tasks require either
many free parameters (e.g., input weights)
or high weight precision (e.g., for continuous-valued parameters),
such that guessing becomes completely infeasible.
Currently it is unclear to which extent more complex
gradient-less methods can improve upon guessing in case of
more realistic tasks.
Bengio et al.'s approaches.
Bengio et al. [6]
investigate methods such as simulated annealing,
multi-grid random search, time-weighted pseudo-Newton
optimization, and discrete error propagation.
Bengio and Frasconi
[4]
also propose an EM approach for propagating targets.
With 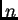 so-called ``state networks'', at a given
time, their system
can be in one of only
so-called ``state networks'', at a given
time, their system
can be in one of only 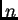 different states.
But to solve problems with continuous-valued inputs
and outputs such systems would require an unacceptable number
of states (i.e., state networks).
different states.
But to solve problems with continuous-valued inputs
and outputs such systems would require an unacceptable number
of states (i.e., state networks).



Next: Probabilistic target propagation
Up: Remedies
Previous: Ring's approach
Juergen Schmidhuber
2003-02-19