


Next: Example Applications
Up: Discussion & Previous Work
Previous: Discussion & Previous Work
Possible Types of Gödel Machine Self-Improvements
Which provably useful self-modifications are possible?
There are few limits to what a Gödel machine might do.
- In one of the simplest cases
it might leave its basic proof searcher intact
and just change the ratio of time-sharing between
the proof searching subroutine and the
subpolicy
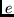 --those parts of
--those parts of 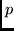 responsible for interaction with the environment.
responsible for interaction with the environment.
- Or the Gödel machine might modify
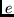 only.
For example, the initial
only.
For example, the initial 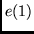 may be a program
that regularly stores limited memories
of past events somewhere in
may be a program
that regularly stores limited memories
of past events somewhere in 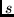 ; this might allow
; this might allow 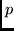 to derive that
it would be useful to modify
to derive that
it would be useful to modify 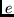 such that
such that 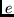 will conduct certain
experiments to increase the knowledge about
the environment, and use the resulting information
to increase reward intake. In this sense the Gödel machine embodies
a principled way of dealing with the
exploration vs exploitation problem [20].
Note that the expected utility (equation (1))
of conducting some experiment may exceed
the one of not conducting it,
even when the experimental outcome later suggests to
keep acting in line with the previous
will conduct certain
experiments to increase the knowledge about
the environment, and use the resulting information
to increase reward intake. In this sense the Gödel machine embodies
a principled way of dealing with the
exploration vs exploitation problem [20].
Note that the expected utility (equation (1))
of conducting some experiment may exceed
the one of not conducting it,
even when the experimental outcome later suggests to
keep acting in line with the previous 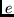 .
.
- The Gödel machine might also modify its very axioms
to speed things up. For example,
it might find a proof that the
original axioms should be replaced or
augmented by theorems derivable
from the original axioms.
- The Gödel machine might even change
its own utility function and target theorem,
but can do so only if their new values
are provably better according to the old ones.
- In many cases we do not expect
the Gödel machine to replace its proof searcher by
code that completely abandons the search for proofs.
Instead we expect that only certain subroutines
of the proof searcher will be sped up--compare the
example in Section 4.4--or that perhaps just
the order of generated proofs will be
modified in problem-specific fashion. This could be done
by modifying
the probability distribution on the proof techniques of
the initial bias-optimal proof searcher
from Section 5.
- Generally speaking,
the utility of limited rewrites may often be
easier to prove than the one of total rewrites.
For example, suppose it is 8.00pm and our Gödel machine-controlled
agent's permanent goal is to
maximize future expected reward, using the (alternative)
target theorem (3). Part thereof is to avoid hunger. There
is nothing in its fridge, and shops close down at 8.30pm. It does not
have time to optimize its way to the supermarket in every little detail,
but if it does not get going right now it will stay hungry tonight (in
principle such near-future consequences of actions should be easily
provable, possibly even in a way related to
how humans prove advantages of potential actions to themselves). That
is, if the agent's previous policy did not already include, say, an automatic
daily evening trip to the supermarket, the policy provably should be
rewritten at least in a very limited and simple way right now, while there
is still time, such that the agent will surely get some food tonight,
without affecting less urgent future behavior that can be optimized
/ decided later, such as details of the route to the food, or
of tomorrow's actions.
- In certain uninteresting environments reward
is maximized by becoming dumb. For example,
a given task may require to repeatedly
and forever execute the same pleasure center-activating action,
as quickly as possible. In such cases the Gödel machine may delete
most of its more time-consuming initial software
including the proof searcher.
- Note that there is no reason why a Gödel machine should not
augment its own hardware.
Suppose its lifetime is known to be 100 years.
Given a hard problem and
axioms restricting the possible
behaviors of the environment,
the Gödel machine might find a proof that its
expected cumulative reward will increase if
it invests 10 years into building faster computational
hardware, by exploiting the physical resources of
its environment.



Next: Example Applications
Up: Discussion & Previous Work
Previous: Discussion & Previous Work
Juergen Schmidhuber
2005-01-03