...Schmidhuber:03gm,Schmidhuber:04gmhtml.¹

Or `Goedel machine', to avoid the Umlaut. But `Godel machine' would not be quite correct. Not to be confused with what Penrose calls, in a different context, `Gödel's putative theorem-proving machine' [30]!

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... machine²

Turing reformulated Gödel's unprovability results in terms of Turing machines (TMs) [56] which subsequently became the most widely used abstract model of computation. It is well-known that there are universal TMs that in a certain sense can emulate any other TM or any other known computer. Gödel's integer-based formal language can be used to describe any universal TM, and vice versa.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... etc.³

We see that certain parts of the current 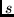$s$ may not be directly observable without changing the observable itself. Sometimes, however, axioms and previous observations will allow the Gödel machine to deduce time-dependent storage contents that are not directly observable. For instance, by analyzing the code being executed through instruction pointer IP in the example above, the value of IP at certain times may be predictable (or postdictable, after the fact). The values of other variables at given times, however, may not be deducible at all. Such limits of self-observability are reminiscent of Heisenberg's celebrated uncertainty principle [12], which states that certain physical measurements are necessarily imprecise, since the measuring process affects the measured quantity.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.