Unless stated otherwise or obvious,
throughout the paper newly introduced variables and functions
are assumed to cover the range implicit in the context.
![]() denotes the binary alphabet
denotes the binary alphabet ![]() ,
,
![]() the set of possible bitstrings over
the set of possible bitstrings over ![]() ,
,
![]() denotes the number of bits in a bitstring
denotes the number of bits in a bitstring ![]() ;
;
![]() the
the ![]() -th bit of
-th bit of ![]() ;
;
![]() the empty string (where
the empty string (where ![]() );
);
![]() if
if ![]() and
and
![]() otherwise (where
otherwise (where
![]() ).
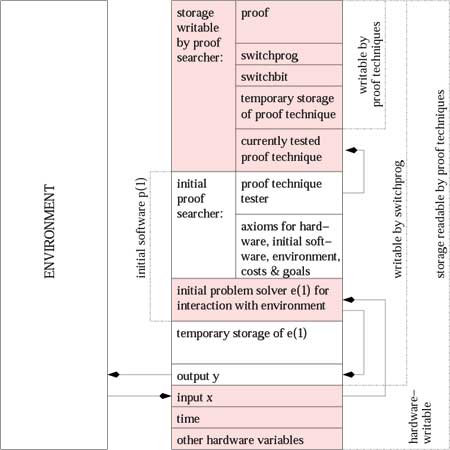
Occasionally it may be convenient
to consult Figure 1 below.
).
Occasionally it may be convenient
to consult Figure 1 below.
 |