DERIVATION OF THE ALGORITHM

Outline. We are interested in weights representing nets with tolerable error but flat outputs (see section 2 and appendix A.1). To find nets with flat outputs, two conditions will be defined to specify $B(w,x_p)$ for $x_p \in X_0$ and, as a consequence, $B(w,X_0)$ (see section 3). The first condition ensures flatness. The second condition enforces ``equal flatness'' in all weight space directions, to obtain low variance of the net functions induced by weights within a box. The second condition will be justified using an MDL-based argument. In both cases, linear approximations will be made (to be justified in A.2).

Formal details. We are interested in weights causing tolerable error (see ``acceptable minima'' in section 2) that can be perturbed without causing significant output changes, thus indicating the presence of many neighboring weights leading to the same net function. By searching for the boxes from section 2, we are actually searching for low-error weights whose perturbation does not significantly change the net function.

In what follows we treat the input $x_p$ as fixed: for convenience, we suppress $x_p$, i.e. we abbreviate $o^k(w,x_p)$ by $o^k(w)$. Perturbing the weights $w$ by $\delta w$ (with components $\delta w_{ij}$), we obtain $ED(w,\delta w) := \sum_{k} (o^k(w + \delta w) - o^k(w))^{2}$, where $o^k(w)$ expresses $o^k$'s dependence on $w$ (in what follows, however, $w$ often will be suppressed for convenience, i.e. we abbreviate $o^k(w)$ by $o^k$). Linear approximation (justified in A.2) gives us ``Flatness Condition 1'':

$$ED(w,\delta w) \approx ED_l(\delta w) := \sum_{k} (\sum_{i,j} \fr... ... o^k}{\partial w_{ij}}\vert \vert \delta w_{ij}\vert)^{2} \leq \epsilon\mbox{,}$$ (3)

where $\epsilon > 0$ defines tolerable output changes within a box and is small enough to allow for linear approximation (it does not appear in $B(w,x_p)$'s and $B(w,D_0)$'s gradient, see section 3). $ED_l$ is $ED$'s linear approximation, and $ED_{l,max}$ is $max \{ED_{l}(w,\delta v)\vert \forall_{ij}\!\!:\delta v_{ij} = \pm \delta w_{ij} \}$. Flatness condition 1 is a ``robustness condition'' (or ``fault tolerance condition'', or ``perturbation tolerance condition'' - see, e.g., Minai & Williams, 1994; Murray & Edwards, 1993; Neti et al., 1992; Matsuoka, 1992; Bishop, 1993; Kerlirzin & Vallet, 1993; Carter et al., 1990).

Many boxes $M_w$ satisfy flatness condition 1. To select a particular, very flat $M_w$, the following ``Flatness Condition 2'' uses up degrees of freedom left by inequality (3):

$$\forall i,j,u,v:(\delta w_{ij})^{2} \sum_{k} (\frac{\partial o^k}... ...delta w_{uv})^{2} \sum_{k} (\frac{\partial o^k}{\partial w_{uv}})^{2} \mbox{ .}$$ (4)

Flatness condition 2 enforces equal ``directed errors''
$ED_{ij}(w,\delta w_{ij}) = \sum_{k} (o^k(w_{ij} + \delta w_{ij}) - o^k(w_{ij}))^{2} \approx \sum_{k} (\frac{\partial o^k}{\partial w_{ij}} \delta w_{ij})^{2}$, where $o^k(w_{ij})$ has the obvious meaning, and $\delta w_{ij}$ is the $i,j$-th component of $\delta w$. Linear approximation is justified by the choice of $\epsilon$ in inequality (3). As will be seen in the MDL-justification to be presented below, flatness condition 2 favors the box which minimizes the mean perturbation error within the box. This corresponds to minimizing the variance of the net functions induced by weights within the box (recall that $ED(w,\delta w)$ is quadratic).

How to derive the algorithm from flatness conditions 1 and 2. We first solve equation (4) for 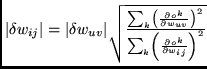$\vert\delta w_{ij}\vert = \vert\delta w_{uv}\vert \sqrt{\frac{\sum_k \left( \f... ...uv}} \right)^2} {\sum_k \left( \frac{\partial o^k}{\partial w_{ij}} \right)^2}}$ (fixing $u,v$ for all $i,j$). Then we insert the $\vert\delta w_{ij}\vert$ (with fixed $u,v$) into inequality (3) (replacing the second ``$\leq$'' in (3) by ``$=$'', since we search for the box with maximal volume). This gives us an equation for the $\vert\delta w_{uv}\vert$ (which depend on $w$, but this is notationally suppressed):

$$\vert\delta w_{uv}\vert = \frac{\sqrt{\epsilon}}{\sqrt{\sum_... ...\partial o^k}{\partial w_{ij}})^{2}} } \right)^{2}}} \mbox{ .}$$ (5)

The $\vert\delta w_{ij}\vert$ ($u,v$ is replaced by $i,j$) approximate the $\Delta w_{ij}$ from section 2. The box $M_w$ is approximated by $AM_w$, the box with center $w$ and edge lengths $2 \delta w_{ij}$. $M_w$'s volume $V(\Delta w)$ is approximated by $AM_w$'s box volume $V(\delta w) :=2^L \prod_{ij} \vert \delta w_{ij} \vert$. Thus, $\tilde B(w,x_p)$ (see section 3) can be approximated by $B(w,x_p):= - \log \frac{1}{2^L} V(\delta w) = \sum_{i,j} - \log \vert \delta w_{ij}\vert$. This immediately leads to the algorithm given by equation (1).

How can the above approximations be justified? The learning process itself enforces their validity (see A.2). Initially, the conditions above are valid only in a very small environment of an ``initial'' acceptable minimum. But during search for new acceptable minima with more associated box volume, the corresponding environments are enlarged. Appendix A.2 will prove this for feedforward nets (experiments indicate that this appears to be true for recurrent nets as well).

Comments. Flatness condition 2 influences the algorithm as follows: (1) The algorithm prefers to increase the $\delta w_{ij}$'s of weights whose current contributions are not important to compute the target output. (2) The algorithm enforces equal sensitivity of all output units with respect to weights of connections to hidden units. Hence, output units tend to share hidden units, i.e., different hidden units tend to contribute equally to the computation of the target. The contributions of a particular hidden unit to different output unit activations tend to be equal, too.

Flatness condition 2 is essential: flatness condition 1 by itself corresponds to nothing more but first order derivative reduction (ordinary sensitivity reduction). However, as mentioned above, what we really want is to minimize the variance of the net functions induced by weights near the actual weight vector.

Automatically, the algorithm treats units and weights in different layers differently, and takes the nature of the activation functions into account.

Back to Financial Forecasting page