FMS details.
To control ![]() 's influence during learning,
its gradient
is normalized and multiplied by the length of
's influence during learning,
its gradient
is normalized and multiplied by the length of
![]() 's gradient (same for weight decay, see below).
's gradient (same for weight decay, see below).
![]() is computed like in (Weigend et al., 1991)
and initialized with 0.
Absolute values of first order derivatives are replaced by
is computed like in (Weigend et al., 1991)
and initialized with 0.
Absolute values of first order derivatives are replaced by
![]() if below this value.
We ought to judge a weight
if below this value.
We ought to judge a weight ![]() as being pruned if
as being pruned if
![]() (see equation (5) in section 4)
exceeds the length of the weight range.
However,
the unknown scaling factor
(see equation (5) in section 4)
exceeds the length of the weight range.
However,
the unknown scaling factor ![]() (see inequality (3) and
equation (5) in section 4)
is required to compute
(see inequality (3) and
equation (5) in section 4)
is required to compute ![]() .
Therefore, we
judge a weight
.
Therefore, we
judge a weight ![]() as being pruned if,
with arbitrary
as being pruned if,
with arbitrary
![]() ,
,
![]() is much bigger than
the corresponding
is much bigger than
the corresponding ![]() 's of the other weights (typically,
there are clearly separable classes of weights with
high and low
's of the other weights (typically,
there are clearly separable classes of weights with
high and low ![]() 's, which differ from each other by a factor
ranging from
's, which differ from each other by a factor
ranging from ![]() to
to ![]() ).
).
If all weights to and from a particular unit are
very close to zero, the unit is lost: due to
tiny derivatives, the weights will never
again increase significantly.
Sometimes, it is necessary to bring lost units back into the game.
For this purpose,
every ![]() time steps (typically,
time steps (typically, ![]() 500,000),
all weights
500,000),
all weights ![]() with
with
![]() are randomly
re-initialized
in
are randomly
re-initialized
in ![]() ; all
weights
; all
weights ![]() with
with
![]() are randomly initialized
in
are randomly initialized
in
![]() ,
and
,
and ![]() is set to 0.
is set to 0.
Weight decay details.
We used Weigend et al.'s weight decay term:
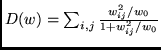 .
Like with FMS,
.
Like with FMS, ![]() 's
gradient was normalized and multiplied by the length of
's
gradient was normalized and multiplied by the length of
![]() 's gradient.
's gradient.
![]() was adjusted like with FMS.
Lost units were brought back
like with FMS.
was adjusted like with FMS.
Lost units were brought back
like with FMS.
Modifications of OBS.
Typically, most weights exceed 1.0 after training.
Therefore, higher order terms of ![]() in the Taylor expansion of the error function
do not vanish.
Hence, OBS is not fully theoretically justified.
Still, we used OBS to delete high weights,
assuming that higher order derivatives are small if
second order derivatives are.
To obtain reasonable performance,
we modified the original OBS procedure
(notation following Hassibi and Stork, 1993):
in the Taylor expansion of the error function
do not vanish.
Hence, OBS is not fully theoretically justified.
Still, we used OBS to delete high weights,
assuming that higher order derivatives are small if
second order derivatives are.
To obtain reasonable performance,
we modified the original OBS procedure
(notation following Hassibi and Stork, 1993):
![$L_q= \frac{w_q^2}{[H^{-1}]_{qq}}$](img167.png) (the original
value used by Hassibi and Stork) and
(the original
value used by Hassibi and Stork) and