- ... DAX1
- Raw DAX version according to
Statistisches Bundesamt (federal office of statistics).
Other data are from the same source (except for business sentiment).
Collected by Christian Puritscher, for a diploma thesis
in industrial management at LMU, Munich.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....2
-
We have
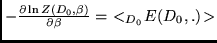 and
and
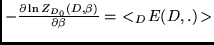 .
Furthermore,
.
Furthermore,
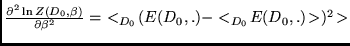 and
and
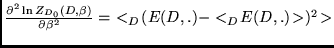 .
See also Levin et al. (1990).
Using these expressions, it can be shown:
by increasing
.
See also Levin et al. (1990).
Using these expressions, it can be shown:
by increasing 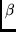 (starting from
(starting from 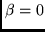 ), we will find a
), we will find a 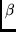 that
minimizes
that
minimizes
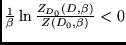 .
Increasing
.
Increasing 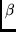 further makes this expression go to
further makes this expression go to 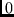 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.