


Next: AN OBJECTIVE FUNCTION FOR
Up: OBJECTIVE FUNCTIONS FOR THE
Previous: OBJECTIVE FUNCTIONS FOR THE
For the sake of argument,
let us assume that at all times each
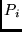 is as good as it can be, meaning that
is as good as it can be, meaning that
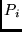 always predicts the expectation of
always predicts the expectation of 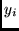 conditioned on the outputs
of the other modules,
conditioned on the outputs
of the other modules,
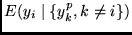 .
(In practice, the predictors will have to be retrained
continually.)
In the case of
quasi-binary codes
the following objective function
.
(In practice, the predictors will have to be retrained
continually.)
In the case of
quasi-binary codes
the following objective function 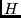 is zero if the
independence criterion is met:
is zero if the
independence criterion is met:
![\begin{displaymath}
H =
\frac{1}{2}
\sum_i \sum_p \left[ P^p_i - \bar{y_i} \right]^2.
\end{displaymath}](img28.png) |
(2) |
This term for mutual predictability minimization aims at making
the outputs independent - similar to the goal of
a term for maximizing the determinant of the
covariance matrix under Gaussian assumptions
(Linsker, 1988). The latter
method, however, tends to remove only linear predictability, while
the former can remove non-linear predictability as well (even without
Gaussian assumptions), due to
possible non-linearities learnable by non-linear predictors.
Juergen Schmidhuber
2003-02-13
Back to Independent Component Analysis page.
![\begin{displaymath}
H =
\frac{1}{2}
\sum_i \sum_p \left[ P^p_i - \bar{y_i} \right]^2.
\end{displaymath}](img28.png)
![\begin{displaymath}
H =
\frac{1}{2}
\sum_i \sum_p \left[ P^p_i - \bar{y_i} \right]^2.
\end{displaymath}](img28.png)