For each representational unit ![]() there corresponds
an adaptive
predictor
there corresponds
an adaptive
predictor ![]() , which, in general, is non-linear.
With the
, which, in general, is non-linear.
With the ![]() -th input pattern
-th input pattern ![]() ,
,
![]() 's
input is the concatenation
of the outputs
's
input is the concatenation
of the outputs ![]() of
all units
of
all units ![]() .
.
![]() 's one-dimensional output
's one-dimensional output ![]() is trained to equal the expectation
is trained to equal the expectation
![]() .
It is well-known that this can be achieved by
letting
.
It is well-known that this can be achieved by
letting ![]() minimize2
minimize2
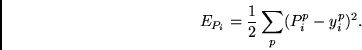 |
(1) |
With the help of the ![]() predictors one can define various
objective functions for the representational modules to
enforce the 3 criteria listed above (see section 4 and section 5).
Common to these methods is that
all units are trained to take on values that
minimize mutual predictability via the predictors:
Each unit tries to extract features from the environment
such that no combination of
predictors one can define various
objective functions for the representational modules to
enforce the 3 criteria listed above (see section 4 and section 5).
Common to these methods is that
all units are trained to take on values that
minimize mutual predictability via the predictors:
Each unit tries to extract features from the environment
such that no combination of ![]() units conveys information
about the remaining unit. In other words,
no combination of
units conveys information
about the remaining unit. In other words,
no combination of ![]() units should allow better
predictions of the remaining unit than a prediction based
on a constant.
I call this the principle
of intra-representational predictability minimization or, somewhat
shorter,
the principle of predictability minimization.
units should allow better
predictions of the remaining unit than a prediction based
on a constant.
I call this the principle
of intra-representational predictability minimization or, somewhat
shorter,
the principle of predictability minimization.
A major novel aspect of this principle which makes it different from previous work is that it uses adaptive sub-modules (the predictors) to define the objective functions for the subjects of interest, namely, the representational units themselves.
Following the principle of predictability minimization, each representational module tries to use the statistical properties of the environment to protect itself from being predictable. This forces each representational module to focus on aspects of the environment that are independent of environmental properties upon which the other modules focus.