This introductory experiment focuses on the totally unsupervised case -- there is no external reinforcement for solving pre-wired tasks. Thus there also is no objective way of measuring the system's performance. The experiment's only purpose is to give an impression of what happens while the active learner is running freely. In what follows I will describe a single but rather typical run.
The entrance to the small room in Figure 2 is blocked.
The system runs for ![]() time steps corresponding to about
time steps corresponding to about ![]() instructions. The system does make heavy use of its arithmetic
instructions: soon the entire storage is filled with
varying numbers generated as by-products of its computations.
instructions. The system does make heavy use of its arithmetic
instructions: soon the entire storage is filled with
varying numbers generated as by-products of its computations.
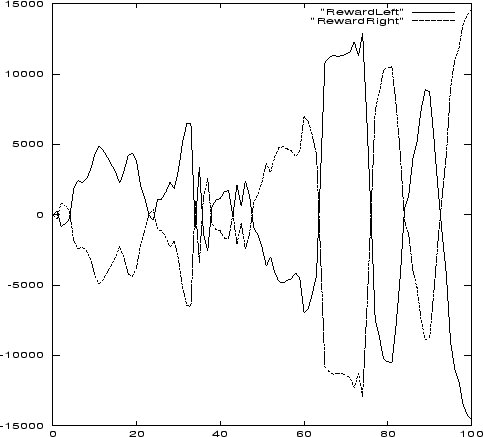
Zero-sum reward. Consider Figure 3. The derivatives of the reward plots at a given time tell which module currently receives more reward than the other. There are long time intervals during which one of the modules dominates. The existence of zero crossings, however, shows that each module occasionally collects sufficient negative rewards to cancel all the previously collected positive rewards, and vice versa. This means that no module consistently outperforms the other.
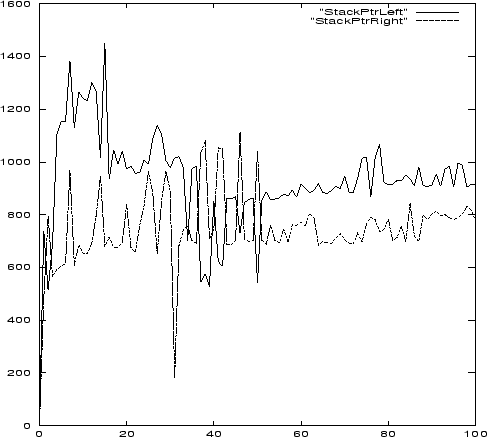
Stack pointer evolution. The stack pointers reflect the number of currently valid module column modifications. Consider Figure 4. Initially the stacks grow very quickly. Then there is a consolidation phase. Later growth resumes, but at a much more modest level -- it becomes harder and harder for each module to acquire additional ``probabilistic knowledge'' to outwit the other. Sometimes SSA pops off a module's entire stack (Figure 4's temporal resolution is too low to show this), but in such cases the stack pointer soon reaches its old value again. This is partly due to SSAandCopy instructions copying the currently superior module onto the other to enforce fair matches.
Reward acceleration. Even in later stages both modules are able to accelerate their long-term average reward intake again and again, despite the fact that the sum of all rewards remains zero. As each module collects a lot of negative reward during its life, it continually pops appropriate checkpoints/modifications off its stack such that the resulting histories of surviving module modifications correspond to histories of less and less negative reward/time ratios. Recall the occasional popping off of the entire stack.
Evolution of instruction frequencies. Consider Figure 5. Although the sum of all surprise rewards remains zero, Bet! instructions are soon among the most frequent types. Other instructions also experience temporary popularity, often in the form of sharp peaks beyond the plot's resolution. Usually, however, the module that does not profit from them learns to put its veto in.
 |
 |
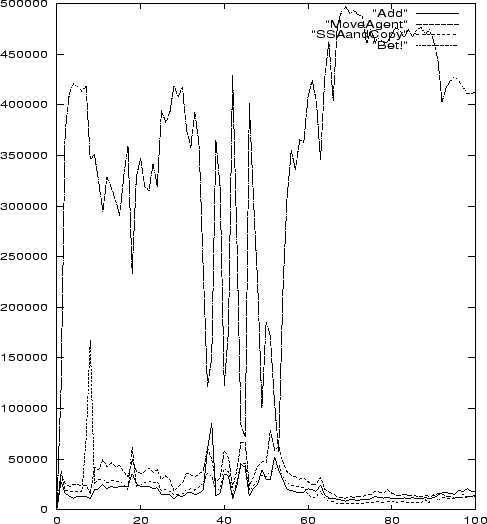 |
Interestingness depends on current knowledge and computational abilities. These are very different for human observers and my particular implementation. It seems hard to trace and understand the system's millions of self-surprises and self-modifications. Figure 5, for instance, provides only very limited insight into the nature of the complex computations carried out. It plots frequencies of selected instruction types but ignores the corresponding arguments and InstructionPointer positions. It does not reflect that for a while computations may focus on just a few module columns and storage cells, until this gets ``boring'' from the system's point of view. Much remains to be done to analyze details of the system's complex dynamics.
Creativity's utility? Can the probabilistic knowledge collected by a ``creative'' two-module system (solving self-generated tasks in an unsupervised manner) help to solve externally posed tasks? The following experiment provides a simple example where this type of curiosity indeed helps to achieve faster goal-directed learning in the case of occasional non-zero environmental reward.