


Next: APPLICATION: IMAGE PROCESSING
Up: SEMILINEAR PREDICTABILITY MINIMIZATION PRODUCES
Previous: INTRODUCTION
In its most simple form,
PM is based on a feedforward network with
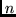 sigmoid output units (or code units).
See Figure 1.
sigmoid output units (or code units).
See Figure 1.
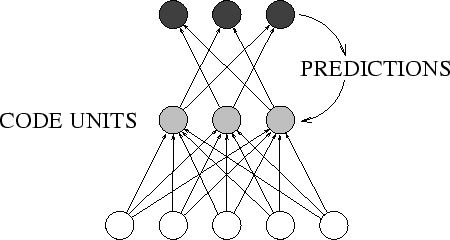
Figure 1:
Predictability minimization (PM):
input patterns with redundant components are coded
across 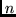 code units (grey). Code units
are also input units of
code units (grey). Code units
are also input units of 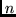 predictor networks.
Each predictor (output units black) attempts to
predict its code unit (which it cannot see).
But each code unit tries to escape the predictions,
by representing environmental properties
that are independent from those
represented by other code units.
This encourages high information throughput and
redundancy reduction. Predictors and code generating net
may have hidden units. In this paper, however, they don't.
See text for details.
predictor networks.
Each predictor (output units black) attempts to
predict its code unit (which it cannot see).
But each code unit tries to escape the predictions,
by representing environmental properties
that are independent from those
represented by other code units.
This encourages high information throughput and
redundancy reduction. Predictors and code generating net
may have hidden units. In this paper, however, they don't.
See text for details.
 |
The  -th code unit produces
a real-valued output value
-th code unit produces
a real-valued output value
![$y^p_i \in [0, 1]$](img11.png) (the
unit interval) in
response to the
(the
unit interval) in
response to the 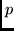 -th external input
vector
-th external input
vector 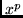 (later we will see that training tends to make
the ouput values near-binary).
There are
(later we will see that training tends to make
the ouput values near-binary).
There are 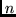 additional feedforward nets
called predictors, each having one
output unit and
additional feedforward nets
called predictors, each having one
output unit and 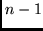 input units.
The predictor for code unit
input units.
The predictor for code unit  is called
is called 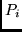 . Its real-valued output in response to the
. Its real-valued output in response to the
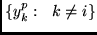 is called
is called 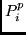 .
.
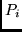 is trained
(in our experiments by conventional online backprop)
to minimize
is trained
(in our experiments by conventional online backprop)
to minimize
 |
(1) |
thus learning to approximate the
conditional expectation
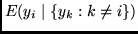 of
of 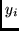 , given the activations of the remaining code units.
Of course, this conditional expectation
typically will be very different from the actual activations
of the code unit. For instance, assume that a certain code unit
will be switched on in one third of all cases within
a given context (defined
by the activations of the remaining code units),
while it will be switched off in two thirds
of all such cases. Then, given this context,
the predictor will predict a value of 0.3333.
, given the activations of the remaining code units.
Of course, this conditional expectation
typically will be very different from the actual activations
of the code unit. For instance, assume that a certain code unit
will be switched on in one third of all cases within
a given context (defined
by the activations of the remaining code units),
while it will be switched off in two thirds
of all such cases. Then, given this context,
the predictor will predict a value of 0.3333.
The clue is:
the code units are trained (in our experiments by online backprop)
to maximize essentially the same objective function
[Schmidhuber, 1992]
the predictors try to minimize:
 |
(2) |
Predictors and code units co-evolve by fighting
each other.
Justification.
Let us assume that the 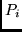 never get trapped in local minima
and always perfectly learn the conditional expectations.
It then turns out that the objective function
never get trapped in local minima
and always perfectly learn the conditional expectations.
It then turns out that the objective function 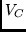 is essentially equivalent to the following one
(also given in Schmidhuber, 1992):
is essentially equivalent to the following one
(also given in Schmidhuber, 1992):
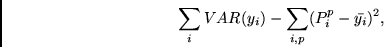 |
(3) |
where 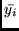 denotes the mean activation of unit
denotes the mean activation of unit  ,
and VAR denotes the variance operator.
The equivalence of (2) and (3) was observed by
Peter Dayan, Richard Zemel and Alex Pouget (personal communication,
SALK Institute, 1992 --
see [Schmidhuber, 1993] for details).
(3) gives some intuition about what is going on while
(2) is maximized.
Mazimizing the first term of (3) tends to enforce binary units,
and also local maximization of information throughput (given
the binary constraint).
Maximizing the second (negative) term
(or minimizing the corresponding unsigned term)
tends to make the conditional
expectations equal to the unconditional expectations, thus
encouraging mutual statistical independence (zero mutual information)
and global maximization of information throughput.
,
and VAR denotes the variance operator.
The equivalence of (2) and (3) was observed by
Peter Dayan, Richard Zemel and Alex Pouget (personal communication,
SALK Institute, 1992 --
see [Schmidhuber, 1993] for details).
(3) gives some intuition about what is going on while
(2) is maximized.
Mazimizing the first term of (3) tends to enforce binary units,
and also local maximization of information throughput (given
the binary constraint).
Maximizing the second (negative) term
(or minimizing the corresponding unsigned term)
tends to make the conditional
expectations equal to the unconditional expectations, thus
encouraging mutual statistical independence (zero mutual information)
and global maximization of information throughput.



Next: APPLICATION: IMAGE PROCESSING
Up: SEMILINEAR PREDICTABILITY MINIMIZATION PRODUCES
Previous: INTRODUCTION
Juergen Schmidhuber
2003-02-17
Back to Independent Component Analysis page.
![]() sigmoid output units (or code units).
See Figure 1.
sigmoid output units (or code units).
See Figure 1.

![]() never get trapped in local minima
and always perfectly learn the conditional expectations.
It then turns out that the objective function
never get trapped in local minima
and always perfectly learn the conditional expectations.
It then turns out that the objective function ![]() is essentially equivalent to the following one
(also given in Schmidhuber, 1992):
is essentially equivalent to the following one
(also given in Schmidhuber, 1992):